题目内容
一家饮料厂生产甲、乙两种果汁饮料,甲种饮料主要配方是每3份李子汁加1份苹果汁,乙种饮料的配方是李子汁和苹果汁各一半.若该厂每天能获得2000L李子汁和1000L苹果汁的原料,且厂方的利润是生产1L甲种饮料得3元,生产1L乙种饮料得4元.那么厂方每天生产甲、乙两种饮料各多少,才能获利最大?
考点:简单线性规划
专题:不等式的解法及应用
分析:根据题意,先确定可行域,建立利润函数,利用数形结合即可得到结论.
解答:
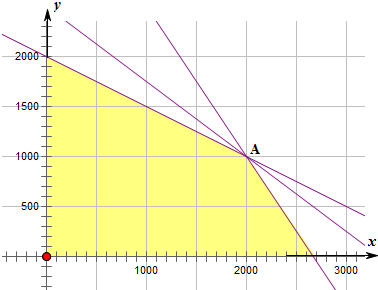 解答:解:设生产x升甲种饮料,y升乙种饮料,
解答:解:设生产x升甲种饮料,y升乙种饮料,
则
,
该厂能获得的利润z=3x+4y,画出可行域,如图.
当直线z=3x+4y经过点A(2000,1000)的时候z值最大,
∴当x=2000,y=1000 时,最大利润z=3×2000+4×1000=10000.
答:厂方每天生产甲2000L、乙1000L时,才能获利最大.
 解答:解:设生产x升甲种饮料,y升乙种饮料,
解答:解:设生产x升甲种饮料,y升乙种饮料,则
|
该厂能获得的利润z=3x+4y,画出可行域,如图.
当直线z=3x+4y经过点A(2000,1000)的时候z值最大,
∴当x=2000,y=1000 时,最大利润z=3×2000+4×1000=10000.
答:厂方每天生产甲2000L、乙1000L时,才能获利最大.
点评:以实际问题为素材,考查生产的最优化,关键在于建立不等式组,同时注意应使实际问题有意义.

练习册系列答案
相关题目
设U=R,若集合M={x|-1<x≤2},则∁UM=( )
| A、(-∞,-1] |
| B、(2,+∞) |
| C、(-∞,-1]∪[2,+∞) |
| D、(-∞,-1]∪(2,+∞) |
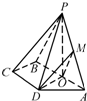 如图,已知四棱锥P-ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO⊥平面ABCD,PO=CD=DA=
如图,已知四棱锥P-ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO⊥平面ABCD,PO=CD=DA=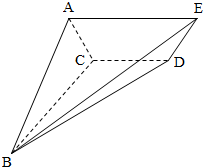 如图,四棱锥B-ACDE中,底面ACDE为直角梯形,CD∥AE,∠BCD=∠ACD=90°,二面角A-CD-B为60°,AE=BC=2,AC=CD=1.
如图,四棱锥B-ACDE中,底面ACDE为直角梯形,CD∥AE,∠BCD=∠ACD=90°,二面角A-CD-B为60°,AE=BC=2,AC=CD=1. 如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2BC=2CD=2.E为AB中点.现将该梯形沿DE析叠.使四边形BCDE所在的平面与平面ADE垂直.
如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2BC=2CD=2.E为AB中点.现将该梯形沿DE析叠.使四边形BCDE所在的平面与平面ADE垂直.