题目内容
已知函数f(x2-3)=loga
(a>1且a≠1).
(1)求函数f(x)的解析式及其定义域;
(2)判断函数f(x)的奇偶性.
| x2 |
| 6-x2 |
(1)求函数f(x)的解析式及其定义域;
(2)判断函数f(x)的奇偶性.
考点:函数解析式的求解及常用方法,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)设t=x2-3,求出f(t)的解析式即得f(x)的解析式,再根据对数的真数大于0,求出f(x)的定义域;
(2)根据函数奇偶性的定义,判断f(x)的奇偶性即可.
(2)根据函数奇偶性的定义,判断f(x)的奇偶性即可.
解答:
解:(1)∵函数f(x2-3)=loga
=loga
,
设t=x2-3,则f(t)=loga
,
即f(x)=loga
;
令
>0,
解得-3<x<3,
∴函数f(x)的定义域为(-3,3);
(2)∵f(x)=loga
,x∈(-3,3);
∴任取x∈(-3,3),则
f(-x)=loga
=-loga
=-f(x),
∴函数f(x)是定义域(-3,3)上的奇函数.
| x2 |
| 6-x2 |
| x2-3+3 |
| 3+3-x2 |
设t=x2-3,则f(t)=loga
| t+3 |
| 3-t |
即f(x)=loga
| 3+x |
| 3-x |
令
| 3+x |
| 3-x |
解得-3<x<3,
∴函数f(x)的定义域为(-3,3);
(2)∵f(x)=loga
| 3+x |
| 3-x |
∴任取x∈(-3,3),则
f(-x)=loga
| 3-x |
| 3+x |
| 3+x |
| 3-x |
∴函数f(x)是定义域(-3,3)上的奇函数.
点评:本题考查了求函数的解析式和定义域的问题,也考查了函数的奇偶性的判断问题,是基础题目.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
| A、若α⊥β,m∥α,则m⊥β |
| B、若m∥α,n∥β,且m∥n,则α∥β |
| C、若m⊥β,α⊥β,则m∥α |
| D、若m⊥α,n⊥β,且m⊥n,则α⊥β |
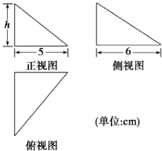 图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=
图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=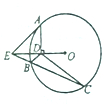 如图,AE是的⊙O切线,A是切点,AD⊥OE于点D,割线EC交⊙O于B,C两点.
如图,AE是的⊙O切线,A是切点,AD⊥OE于点D,割线EC交⊙O于B,C两点.