题目内容
3．直线l过点A（1，1），且l在y轴上的截距的取值范围为（0，2），则直线l的斜率的取值范围为（-1，1）．分析 设直线l的方程为：y-1=k（x-1），化为：y=kx+1-k，由题意可得：0＜1-k＜2．
解答 解：设直线l的方程为：y-1=k（x-1），化为：y=kx+1-k，
由题意可得：0＜1-k＜2，
解得-1＜k＜1．
∴直线l的斜率的取值范围为（-1，1）．
故答案为：（-1，1）．
点评 本题考查了直线的点斜式、截距的应用，考查了推理能力与计算能力，属于基础题．
练习册系列答案
科学实验活动册系列答案
相关题目
13．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}x，x＞0}\\{（\frac{1}{3}）^{x}-2，x≤0}\end{array}\right.$，则不等式f（x）≥1的解集为（ ）
| A． | {x|x≤-1} | B． | {x|x≥3} | C． | {x|x≤-1或x≥3} | D． | {x|x≤0或x≥3} |
14．如图，正三棱柱（底面为正三角形，侧棱垂直底面）的正视图面积a2，则侧视图的面积为（ ）
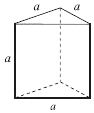
| A． | a2 | B． | $\frac{{\sqrt{3}}}{2}{a^2}$ | C． | $\sqrt{3}{a^2}$ | D． | $\frac{{\sqrt{3}}}{4}{a^2}$ |
18．若直线l经过A（2，1），B（1，-m2）（m∈R）两点，则直线l的倾斜角α的取值范围是（ ）
| A． | 0≤α≤$\frac{π}{4}$ | B． | $\frac{π}{2}$＜α＜π | C． | $\frac{π}{4}$≤α＜$\frac{π}{2}$ | D． | $\frac{π}{2}$＜α≤$\frac{3π}{4}$ |
8．已知平面向量$\overrightarrow a$，$\overrightarrow b$，$|{\overrightarrow a}|=1$，$|{\overrightarrow b}|=\sqrt{2}$，$\overrightarrow a•\overrightarrow b=1$，则向量$\overrightarrow a$，$\overrightarrow b$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{2}$ |
15．
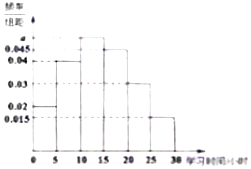某市教育局随机调查了300名高中学生周末的学习时间（单位：小时），制成了如图所示的频率分布直方图，其中学习时间的范围是[0，30]，样本数据分组为，[0，5），[5，10），[10，15），[15，20），[20，25），[25，30]，根据直方图，这300名高中生周末的学习时间是[5，15）小时的人数是（ ）
某市教育局随机调查了300名高中学生周末的学习时间（单位：小时），制成了如图所示的频率分布直方图，其中学习时间的范围是[0，30]，样本数据分组为，[0，5），[5，10），[10，15），[15，20），[20，25），[25，30]，根据直方图，这300名高中生周末的学习时间是[5，15）小时的人数是（ ）| A． | 15 | B． | 27 | C． | 135 | D． | 165 |
13．直角△ABC的三个顶点在半径为R的球面上，两直角边的长分别为6和8，球心到平面ABC的距离是12，则R=（ ）
| A． | 26 | B． | 20 | C． | 13 | D． | 10 |