题目内容
12.已知一家电子公司生产某种电子产品的月固定成本为20万元,每生产1千件需另投入5.4万元,设该公司一月内生产该电子产品x千件能全部销售完,每千件的销售收入为g(x)万元,且g(x)=$\left\{\begin{array}{l}{13.5-\frac{1}{30}{x}^{2}(0<x≤10)}\\{\frac{168}{x}-\frac{2000}{3{x}^{2}}(x>10)}\end{array}\right.$(Ⅰ)写出月利润y(万元)关于月产量x(千件)的函数解析式;
(Ⅱ)月产量为多少千件时,该公司在这一产品的生产中所获利润最大?并求出最大利润.
分析 (Ⅰ)根据年利润=年销售收入-年总成本,可得年利润y(万元)关于年产量x(万件)的函数关系式;
(Ⅱ)由(Ⅰ)的解析式,我们求出各段上的最大值,即利润的最大值,然后根据分段函数的最大值是各段上最大值的最大者,即可得到结果.
解答 解:(Ⅰ)当0<x≤10时,y=x(13.5-$\frac{1}{30}$x2)-20-5.4x=8.1x-$\frac{1}{30}$x3-20,
当x>10时,y=($\frac{168}{x}$--$\frac{2000}{3{x}^{2}}$)x-20-5.4x=148-2($\frac{1000}{3x}$+2.7x),
∴y=$\left\{\begin{array}{l}{8.1x-\frac{1}{30}{x}^{3}-20,0<x≤10}\\{148-2(\frac{1000}{3x}+2.7x),x>10}\end{array}\right.$,
(Ⅱ)①当0<x≤10时,y′=8.1-$\frac{1}{10}$x2,令y′=0可得x=9,
x∈(0,9)时,y′>0;x∈(9,10]时,y′<0,
∴x=9时,ymax=28.6万元;
②当x>10时,y=148-2($\frac{1000}{3x}$+2.7x)≤148-120=22(万元)
(当且仅当x=$\frac{100}{9}$时取等号)…(10分)
综合①②知:当x=9时,y取最大值…(11分)
故当年产量为9万件时,服装厂在这一高科技电子产品的生产中获年利润最大…(12分)
点评 本题考查的知识点是分段函数及函数的最值,分段函数分段处理,这是研究分段函数图象和性质最核心的理念,具体做法是:分段函数的定义域、值域是各段上x、y取值范围的并集,分段函数的奇偶性、单调性要在各段上分别论证;分段函数的最大值,是各段上最大值中的最大者.

 阅读快车系列答案
阅读快车系列答案| A. | {2,4,5} | B. | {1,2,4,5} | C. | {2,5} | D. | {0,2,3,4,5} |
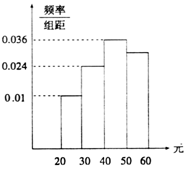 为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )
为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )| A. | 10 | B. | 12 | C. | 15 | D. | 18 |
| A. | $\frac{b-a}{2}$ | B. | $\frac{b+a}{2}$ | C. | $\frac{1-b}{2}$ | D. | $\frac{1-a}{2}$ |
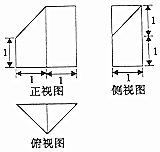
| A. | $\frac{9}{2}$+4$\sqrt{2}$ | B. | 5$+4\sqrt{2}$ | C. | 6$+4\sqrt{2}$ | D. | $\frac{13}{2}$$+4\sqrt{2}$ |
| A. | 偶函数,且在(0,+∞)上是增函数 | |
| B. | 偶函数,且在(0,+∞)上是减函数 | |
| C. | 奇函数,且在(0,+∞)上是增函数 | |
| D. | 非奇非偶函数,且在(0,+∞)上是增函数 |