题目内容

13．直角△ABC的三个顶点在半径为R的球面上，两直角边的长分别为6和8，球心到平面ABC的距离是12，则R=（　　）
A．26B．20C．13D．10

分析 利用已知条件可计算出Rt△ABC的斜边长，根据斜边是Rt△ABC所在截面的直径，进而根据球心到平面ABC的距离，可求得R．

解答 解：Rt△ABC的斜边长为10，Rt△ABC的三个顶点在半径为13的球面上，
∴斜边是Rt△ABC所在截面圆的直径，
∵球心到平面ABC的距离是12，
∴R=$\sqrt{25+144}$=13，
故选：C．

点评 本题主要考查了点到面的距离．解题的关键是利用了斜边是Rt△ABC所在截面的直径这一特性．

练习册系列答案
相关题目
3．直线l过点A（1，1），且l在y轴上的截距的取值范围为（0，2），则直线l的斜率的取值范围为（-1，1）．
4．已知随机变量X～N（6，1），且P（5＜X＜7）=a，P（4＜X＜8）=b，则P（4＜X＜7）=（　　）
A．$\frac{b-a}{2}$B．$\frac{b+a}{2}$C．$\frac{1-b}{2}$D．$\frac{1-a}{2}$
1．一个几何体的三视图如图所示，则其表面积为（　　）
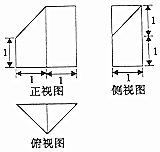
A．$\frac{9}{2}$+4$\sqrt{2}$B．5$+4\sqrt{2}$C．6$+4\sqrt{2}$D．$\frac{13}{2}$$+4\sqrt{2}$
8．关于x的方程（$\frac{1}{3}$）|x|+a-1=0有解，则a的取值范围是（　　）
A．0≤a＜1B．-1＜a≤0C．a≥1D．a＞0
18．“a≤0”是“函数f（x）=|x（ax+1）|在区间（-∞，0）内单调递减”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
5．已知F1，F2是椭圆$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1的两个焦点，经过点F2的直线交椭圆于A，B两点，若|AB|=4，则|AF1|+|BF1|=（　　）
A．12B．9C．8D．2
2．幂函数y=f（x）的图象经过点$（3，\root{3}{3}）$，则f（x）是（　　）
A．偶函数，且在（0，+∞）上是增函数
B．偶函数，且在（0，+∞）上是减函数
C．奇函数，且在（0，+∞）上是增函数
D．非奇非偶函数，且在（0，+∞）上是增函数
3．直线2x-y-2=0绕它与y轴的交点逆时针旋转$\frac{π}{2}$所得的直线方程是（　　）
A．-x+2y-4=0B．x+2y-4=0C．-x+2y+4=0D．x+2y+4=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网