题目内容
8.已知平面向量$\overrightarrow a$,$\overrightarrow b$,$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=\sqrt{2}$,$\overrightarrow a•\overrightarrow b=1$,则向量$\overrightarrow a$,$\overrightarrow b$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
分析 由条件利用两个向量的数量积的定义,求得向量$\overrightarrow a$,$\overrightarrow b$的夹角的余弦值,可得向量$\overrightarrow a$,$\overrightarrow b$的夹角.
解答 解:设向量$\overrightarrow a$,$\overrightarrow b$的夹角为θ,
∵$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=\sqrt{2}$,$\overrightarrow a•\overrightarrow b=1$,
∴1×$\sqrt{2}$×cosθ=1,
∴cosθ=$\frac{\sqrt{2}}{2}$,
结合θ∈[0,π],可得θ=$\frac{π}{4}$,
故选:C.
点评 本题主要考查两个向量的数量积的定义,属于基础题.

练习册系列答案
相关题目
19.小明同学计划两次购买同一种笔芯(两次笔芯的单价不同),有两种方案:第一种方法是每次购买笔芯数量一定:第二种方法是每次购买笔芯所花钱数一定.则哪种购买方式比较经济( )
| A. | 第一种 | B. | 第二种 | C. | 两种一样 | D. | 无法判断 |
13.已知i为虚数单位,复数z满足$3z+\overline z=\frac{4}{1-i}$,则z=( )
| A. | $\frac{1}{4}+\frac{1}{2}i$ | B. | $\frac{1}{2}+i$ | C. | $\frac{1}{4}-\frac{1}{2}i$ | D. | $\frac{1}{2}-i$ |
20.设集合U={0,1,2,3,4,5},A={0,1,3},B={1,2,5},则(∁UA)∩B=( )
| A. | {2,4,5} | B. | {1,2,4,5} | C. | {2,5} | D. | {0,2,3,4,5} |
17.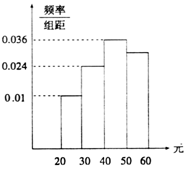 为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )
为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )
 为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )
为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )| A. | 10 | B. | 12 | C. | 15 | D. | 18 |
18.“a≤0”是“函数f(x)=|x(ax+1)|在区间(-∞,0)内单调递减”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |