题目内容
已知a>0且a≠1,指数函数y=ax在(-∞,+∞)上是增函数;如果函数f(x)=log
x在区间[a,2a]上的最大值与最小值之差为
,求实数a的值.
| 1 |
| a |
| 1 |
| 2 |
考点:对数函数的单调性与特殊点
专题:函数的性质及应用
分析:因为y=ax在(-∞,+∞)上是增函数,所以a>1,所以f(x)=log
x在[a,2a]上为减函数,结合函数f(x)=log
x在区间[a,2a]上的最大值与最小值之差为
,构造方程,可得答案.
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
解答:
解:因为y=ax在(-∞,+∞)上是增函数,
所以a>1,…(2分)
所以f(x)=log
x在[a,2a]上为减函数,…(4分)
从而得f(a)-f(2a)=
即log
a-log
2a=
…(6分)
所以log
2=-
,…(10分)
所以(
)-
=2,…(12分)
解得a=4.…(14分)
所以a>1,…(2分)
所以f(x)=log
| 1 |
| a |
从而得f(a)-f(2a)=
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
所以log
| 1 |
| a |
| 1 |
| 2 |
所以(
| 1 |
| a |
| 1 |
| 2 |
解得a=4.…(14分)
点评:本题考查的知识点是指数函数的图象和性质,对数函数的图象和性质,难度不大,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
若圆C的半径为1,点C与点(2,0)关于点(1,0)对称,则圆C的标准方程为( )
| A、x2+y2=1 |
| B、(x-3)2+y2=1 |
| C、(x-1)2+y2=1 |
| D、x2+(y-3)2=1 |
下列程序运行后的输出结果为( )


| A、12 | B、36 | C、48 | D、144 |
下列不等式中不一定成立的是( )
A、lgx+
| ||||
B、x,y>0时,
| ||||
C、
| ||||
D、a>0时,(a+1)(
|
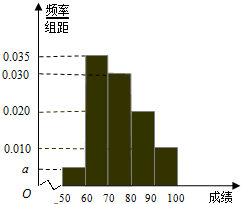 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下: