题目内容
19.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,坐标原点到直线AB的距离为$\frac{\sqrt{3}}{2}$,其中A(0,-b),B(a,0).(1)求双曲线的标准方程;
(2)设F是双曲线的右焦点,直线l过点F且与双曲线的右支交于不同的两点P、Q,|PQ|=10.求直线l的方程.
分析 (1)利用双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,坐标原点到直线AB的距离为$\frac{\sqrt{3}}{2}$,建立方程,求出a,b,即可求双曲线的标准方程;
(2)设直线方程为y=k(x-2),代入双曲线方程,整理可得(3-k2)x2+4k2x-(4k2+3)=0,利用韦达定理,及弦长公式,建立方程,即可求直线l的方程.
解答 解:(1)直线AB的方程为bx-ay-ab=0.
∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,坐标原点到直线AB的距离为$\frac{\sqrt{3}}{2}$,
∴$\frac{{a}^{2}+{b}^{2}}{{a}^{2}}$=4,$\frac{ab}{\sqrt{{b}^{2}+{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,∴a=1,b=$\sqrt{3}$,
∴双曲线的标准方程是${x}^{2}-\frac{{y}^{2}}{3}$=1;
(2)设直线方程为y=k(x-2)
代入双曲线方程,整理可得(3-k2)x2+4k2x-(4k2+3)=0
设P(x1,y1),Q(x2,y2),则可得x1+x2=-$\frac{4{k}^{2}}{3-{k}^{2}}$,x1x2=-$\frac{4{k}^{2}+3}{3-{k}^{2}}$,
∵|PQ|=10,
∴(1+k2)2•[(-$\frac{4{k}^{2}}{3-{k}^{2}}$)2-4(-$\frac{4{k}^{2}+3}{3-{k}^{2}}$)]=100
解得,k=±$\frac{\sqrt{6}}{2}$,
∴直线l的方程为y=±$\frac{\sqrt{6}}{2}$(x-2).
点评 本题考查双曲线的方程与性质,考查直线与双曲线位置关系的运用,考查弦长的计算,属于中档题.

| A. | -$\frac{9}{4}$ | B. | -$\frac{5}{2}$ | C. | $\frac{9}{4}$ | D. | $\frac{5}{2}$ |
 如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.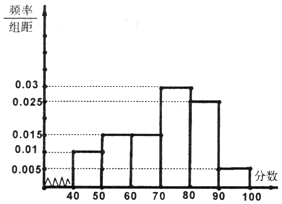 某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题: