题目内容
2.如果二面角α-L-β的大小是60°,线段AB在α内,AB与L所成的角为60°,则AB与平面β所成角的正切值是$\frac{{3\sqrt{7}}}{7}$.分析 过点A作平面β的垂线,垂足为C,在β内过C作CD⊥l于D,连结AD,由三垂线定理证出AD⊥l,可得∠ADC为二面角α-L-β的平面角.连线CB,由AC⊥β可得∠ABC为AB与平面β所成的角,再利用解直角三角形知识,结合题中数据加以计算即可得出求出AB与平面β所成角的正弦值,根据同角三角函数的基本关系,即可AB与平面β所成角的正切值.
解答  解:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线,垂足为D.
解:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线,垂足为D.
连结AD,根据三垂线定理可得AD⊥L,
因此,∠ADC为二面角α-L-β的平面角,∠ADC=60°
又∵AB与L所成角为60°,
∴∠ABD=60°,
连结BC,可得BC为AB在平面β内的射影,
∴∠ABC为AB与平面β所成的角.
设AD=2x,则Rt△ACD中,AC=ADsin60°=$\sqrt{3}$x,
Rt△ABD中,AB=$\frac{AD}{sin60°}$=$\frac{4\sqrt{3}}{3}$x
∴Rt△ABC中,sin∠ABC=$\frac{AC}{AB}$=34,
∴tan∠ABC=$\frac{{3\sqrt{7}}}{7}$
故答案为:$\frac{{3\sqrt{7}}}{7}$.
点评 本题考查了二面角的平面角,考查了线面角,考查同角三角函数的基本关系,考查了学生的空间想象和思维能力,是中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
13.已知点A的坐标为(5,2),F为抛物线y2=x的焦点,若点P在抛物线上移动,当|PA|+|PF|取得最小值时,则点P的坐标是( )
| A. | (1,$\sqrt{2}$) | B. | ($\sqrt{2}$,2) | C. | ($\sqrt{2}$,-2) | D. | (4,2) |
14.如果|x|≤$\frac{π}{4}$,那么函数y=cos2x-3cosx+2的最小值是( )
| A. | 2 | B. | $-\frac{1}{4}$ | C. | 0 | D. | $\frac{{5-3\sqrt{2}}}{2}$ |
12.“今天北京的降雨概率是80%,上海的降雨概率是20%”,下列说法不正确的是( )
| A. | 北京今天一定降雨,而上海一定不降雨 | |
| B. | 上海今天可能降雨,而北京可能没有降雨 | |
| C. | 北京和上海都可能没降雨 | |
| D. | 北京降雨的可能性比上海大 |
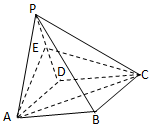 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点.