题目内容
设O是三角形ABC内一点,
+2
+k
=
,且S△AOC:S△ABC=2:11,求k的值.
| OA |
| OB |
| OC |
| 0 |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:构造平行四边形,根据平行四边形的性质得
=
=
=2,再根据相似三角形的面积比,得到S△AOC:S△ABC=2:11=6:(9+3k),解得即可
| EF |
| FO |
| AF |
| FB |
| AE |
| OB |
解答:
解:如图所示,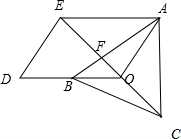
作
=2
,以OA,OB为邻边作平行四边形OAED,
∴
=
+2
=-k
,
由平行四边形的性质可得
=
=
=2,
∴|
|=
|
|=
|
|,k>0,
∴S△AOC=
S△AFC=
×
×2S△ABC,
∴S△AOC:S△ABC=2:11=6:(9+3k),
解得k=8.

作
| OD |
| OB |
∴
| OE |
| OA |
| OB |
| OC |
由平行四边形的性质可得
| EF |
| FO |
| AF |
| FB |
| AE |
| OB |
∴|
| OF |
| 1 |
| 3 |
| OE |
| k |
| 3 |
| CO |
∴S△AOC=
| 3 |
| 3+k |
| 3 |
| 3+k |
| 2 |
| 3 |
∴S△AOC:S△ABC=2:11=6:(9+3k),
解得k=8.
点评:本题考查了向量的平行四边形法则、平行四边形的性质、三角形的面积之比,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知抛物线C:y2=2x上一点P到y轴的距离为3,则 P到焦点的距离为( )
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
如图,△ABC内接于⊙O于A,AD切⊙O于A,∠BAD=60°,则∠ACB=( )


| A、120° | B、150° |
| C、90° | D、100° |
某企业三月中旬生产A、B、C三种产品共3000件,根据分层抽样的结果,企业统计员制作了如下的统计表格.由于不小心,表格中A、C产品的有关数据己被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10件,根据以上信息,可得C产品的数量是( )
| 产品类别 | A | B | C |
| 产品数量(件) | 1300 | ||
| 样本容量(件) | 130 |
| A、900件 | B、800件 |
| C、90件 | D、80件 |
若以点F1(-2,0)、F2(2,0)为焦点的双曲线C过直线l:x+y-1=0上一点M,则能使所作双曲线C的实轴长最长时的双曲线方程为( )
A、x2-
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
对?x1,x2∈(0,
),若x2>x1,且y1=
,y2=
,则( )
| π |
| 2 |
| 1+sinx1 |
| x1 |
| 1+sinx2 |
| x2 |
| A、y1=y2 |
| B、y1>y2 |
| C、y1<y2 |
| D、y1,y2的大小关系不能确定 |