题目内容
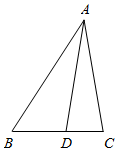
7.已知AD是△ABC中∠A的角平分线,且cos2A+5cosA=2,△ADC与△ADB的面积之比为1:2(1)求sin∠A的值;
(2)求sin∠ADC的值.
分析 (1)根据二倍角公式求出cosA,从而求出sinA即可;(2)设CD=m,AC=n,由余弦定理求出m,n的关系,结合正弦定理求出∠ADC的正弦值即可.
解答 解:(1)△ABC中,∵cos2A=2cos2A-1,
∴由cos2A+5cosA=2得:cosA=$\frac{1}{2}$或cosA=-3(舍),
∴sinA=$\frac{\sqrt{3}}{2}$;
(2)∵$\frac{{S}_{△ADC}}{{S}_{△ADB}}$=$\frac{1}{2}$,∴$\frac{CD}{BD}$=$\frac{1}{2}$,
∵AD是△ABC中∠A的角平分线,
∴$\frac{AC}{AB}$=$\frac{1}{2}$,
设CD=m,AC=n,
由余弦定理得:CB2=AC2+AB2-2AC•AB•cos60°,
即得:n=$\sqrt{3}$m,
由正弦定理得:$\frac{CD}{sin∠CAD}$=$\frac{AC}{sin∠ADC}$,
∴sin∠ADC=$\frac{\sqrt{3}}{2}$.
点评 本题考查了正弦定理、余弦定理的应用,考查二倍角公式,是一道中档题.

练习册系列答案
相关题目
15.在△ABC中,∠C=90°,$\overrightarrow{BA}$=(k,1),$\overrightarrow{BC}$=(2,3),则k的值是( )
| A. | 5 | B. | -5 | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
 在△ABC中,角A,B,C的对应边分别为a,b,c,且三角形的面积为S=$\frac{{\sqrt{3}}}{2}$accosB.
在△ABC中,角A,B,C的对应边分别为a,b,c,且三角形的面积为S=$\frac{{\sqrt{3}}}{2}$accosB.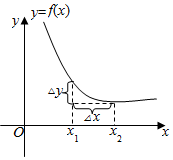 已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.
已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.