题目内容
12.数列{an}中,a1=1,an+1=3an+4,则数列{an}的前n项和等于( )| A. | $\frac{{3}^{n+1}-4n-3}{2}$ | B. | $\frac{{3}^{n}-2n-1}{2}$ | C. | $\frac{{3}^{n}-2n+1}{2}$ | D. | 3n+1-2n-1 |
分析 由an+1=3an+4,变形为:an+1+2=3(an+2),利用等比数列的通项公式、前n项和公式即可得出.
解答 解:由an+1=3an+4,变形为:an+1+2=3(an+2),
∴数列{an+2}是等比数列,首项为3,公比为3.
∴an+2=3n,即an=3n-2,
∴数列{an}的前n项和=$\frac{3({3}^{n}-1)}{3-1}$-2n=$\frac{{3}^{n+1}-4n-3}{2}$.
故选:A.
点评 本题考查了等比数列的通项公式、前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
3.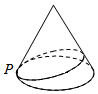 如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )
如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )
 如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )
如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )| A. | 1m | B. | $\frac{3}{2}m$ | C. | $\frac{4}{3}m$ | D. | 2m |
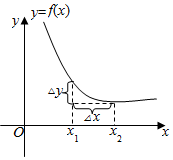 已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.
已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.