题目内容
7.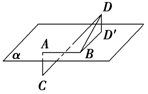 如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.
如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.
分析 通过向量表示出CD向量,然后求模即可得到结果.
解答 解:线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α,∠DBD′=30°,AB=AC=BD=1,
由题意可知:$\overrightarrow{CD}$=$\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,
∴${\overrightarrow{CD}}^{2}$=$(\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD})^{2}$=${\overrightarrow{CA}}^{2}+{\overrightarrow{AB}}^{2}+{\overrightarrow{BD}}^{2}$+$2\overrightarrow{CA}•\overrightarrow{AB}$+$2\overrightarrow{CA}•\overrightarrow{BD}$+$2\overrightarrow{AB}•\overrightarrow{BD}$
=12+12+12+2•12cos60°
=4.
∴所求C、D间的距离为:2.
故答案为2.
点评 本题考查空间向量求解两点间距离的方法之一,考查计算能力.

练习册系列答案
相关题目
2.已知空间四边形OABC,M,N分别是对边OA,BC的中点,点G在线段MN上,且,设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x,y,z的值分别是( )
| A. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ | B. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{6}$ | C. | x=$\frac{1}{3}$,y=$\frac{1}{6}$,z=$\frac{1}{3}$ | D. | x=$\frac{1}{6}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ |
12.“a≠1或b≠3”是“a•b≠3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
19.函数f(x)=$\frac{ln(x+2)}{\sqrt{x-1}}$的定义域为( )
| A. | (-2,+∞) | B. | (1,+∞) | C. | (-2,1) | D. | [1,+∞) |
16.命题“?x>0,总有(x+1)ex>1”的否定是 ( )
| A. | ?x>0,总有(x+1)ex≤ | B. | ?x≤0,总有(x+1)ex≤1 | ||
| C. | ?x0≤0,使得(x0+1)ex0≤1 | D. | ?x0>0,使得(x0+1)ex0≤1 |
17.已知a,b,c∈R,则“b2-4ac<0”是“关于x的不等式ax2+bx+c<0在R上恒成立”的 ( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |