题目内容
19.函数f(x)=$\frac{ln(x+2)}{\sqrt{x-1}}$的定义域为( )| A. | (-2,+∞) | B. | (1,+∞) | C. | (-2,1) | D. | [1,+∞) |
分析 由根式内部的代数式大于等于0,分式的分母不为0联立不等式组求解.
解答 解:由$\left\{\begin{array}{l}{x+2>0}\\{x-1>0}\end{array}\right.$,解得:x>1.
∴函数f(x)=$\frac{ln(x+2)}{\sqrt{x-1}}$的定义域为(1,+∞).
故选:B.
点评 本题考查函数的定义域及其求法,是基础的计算题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
9.函数$f(x)=\sqrt{{x^2}+4x-12}$的单调减区间为( )
| A. | [-2,+∞) | B. | (-∞,-2] | C. | (-∞,-6] | D. | [2,+∞) |
14.已知函数f(x)=x-2sinx,则$f({-\frac{π}{6}})、f({-1})、f({{{log}_3}1.2})$的大小关系为( )
| A. | $f({{{log}_3}1.2})>f({-\frac{π}{6}})>f({-1})$ | B. | $f({-\frac{π}{6}})>f({{{log}_3}1.2})>f({-1})$ | ||
| C. | $f({-\frac{π}{6}})>f({-1})>f({{{log}_3}1.2})$ | D. | $f({-1})>f({-\frac{π}{6}})>f({{{log}_3}1.2})$ |
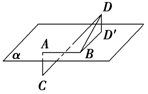 如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.
如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.