题目内容
15.函数$f(x)=cos(x-\frac{π}{2})+sin(x+\frac{π}{3})$的单调递增区间为$(2kπ-\frac{2π}{3},2kπ+\frac{π}{3})k∈Z$.分析 利用三角函数恒等变换的应用化简函数解析式可得f(x)=$\sqrt{3}$sin(x+$\frac{π}{6}$),令2kπ-$\frac{π}{2}$≤x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,即可解得单调递增区间.
解答 解:∵$f(x)=cos(x-\frac{π}{2})+sin(x+\frac{π}{3})$=sinx+$\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx=$\sqrt{3}$sin(x+$\frac{π}{6}$),
令2kπ-$\frac{π}{2}$≤x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,解得:2kπ-$\frac{2π}{3}$≤x≤2kπ+$\frac{π}{3}$,k∈Z,
∴函数$f(x)=cos(x-\frac{π}{2})+sin(x+\frac{π}{3})$的单调递增区间为:$(2kπ-\frac{2π}{3},2kπ+\frac{π}{3})k∈Z$.
故答案为:$(2kπ-\frac{2π}{3},2kπ+\frac{π}{3})k∈Z$.
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的单调性的应用,考查了转化思想和数形结合思想的应用,属于基础题.

练习册系列答案
相关题目
5.已知命题“若p,则q”,假设其逆命题为真,则p是q的( )
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 既不是充分条件也不是必要条件 | D. | 无法判断 |
6.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,m∥β,则α∥β | D. | 若m∥α,α⊥β,则m⊥β |
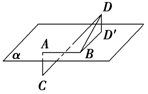 如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.
如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.