题目内容
在等差数列{an}中,a1=-2014,其前n项和为Sn,若
-
=2,则S2014的值为( )
| S12 |
| 12 |
| S10 |
| 10 |
| A、-2011 |
| B、-2012 |
| C、-2013 |
| D、-2014 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:设等差数列的公差为d,利用等差数列的求和公式及
-
=2可求得公差d,再用求和公式可得答案.
| S12 |
| 12 |
| S10 |
| 10 |
解答:
解:设等差数列的公差为d,
∵
-
=2,
∴
-
=2,
∴a12-a10=4,
∴2d=4,得d=2,
∵a1=-2014,
∴S2014=-2014×2014+
×2=-2014,
故选:D.
∵
| S12 |
| 12 |
| S10 |
| 10 |
∴
12×
| ||
| 12 |
10×
| ||
| 10 |
∴a12-a10=4,
∴2d=4,得d=2,
∵a1=-2014,
∴S2014=-2014×2014+
| 2014×2013 |
| 2 |
故选:D.
点评:本题考查等差数列的求和公式,属基础题,熟记等差数列的求和公式是解决该题的关键.

练习册系列答案
相关题目
下列各函数中,是偶函数且在区间(0,π)上为增函数的是( )
| A、y=cosx |
| B、y=sinx |
| C、y=-cosx |
| D、y=-cos2x |
已知lg(x+y)+lg(2x+3y)-lg3=lg4+lgx+lgy,则
的值( )
| x |
| y |
| A、3 | ||
B、3或
| ||
C、
| ||
| D、3或0 |
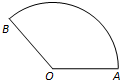 如图,扇形OAB中,OA=OB=1,
如图,扇形OAB中,OA=OB=1, |
| AB |
 |
| AB |
A、1-
| ||
B、2-
| ||
C、1-
| ||
D、
|
已知集合A={x|x2-11x+10≤0},B={y|y=lgx,x∈A},则A∪B=( )
| A、[0,1] |
| B、[1,10] |
| C、{1} |
| D、[0,10] |
 某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.
某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.| A、11 | B、13 | C、15 | D、17 |
设p:“x,y,z中至少有一个等于1”?“(x-1)(y-1)(z-1)=0”;q:“
+|y-2|+(z-3)2=0”?“(x-1)(y-2)(z-3)=0”,那么p,q的真假是( )
| x-1 |
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
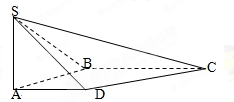 在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC=
在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC=