题目内容
在△ABC中,cos2
=
(a,b,c分别是角A,B,C的对边),则△ABC的形状为( )
| A |
| 2 |
| b+c |
| 2c |
| A、等腰直角三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等边三角形 |
考点:三角形的形状判断
专题:解三角形
分析:由降幂公式和余弦定理化简可得勾股定理的式子,可得结论.
解答:
解:∵cos2
=
,
∴
=
,
∴c(1+cosA)=b+c,
∴c(1+
)=b+c,
∴c•
=b+c,
化简可得b2+c2-a2+2bc=2b2+2bc,
∴c2=a2+b2,∴△ABC为直角三角形,
故选:B.
| A |
| 2 |
| b+c |
| 2c |
∴
| 1+cosA |
| 2 |
| b+c |
| 2c |
∴c(1+cosA)=b+c,
∴c(1+
| b2+c2-a2 |
| 2bc |
∴c•
| b2+c2-a2+2bc |
| 2bc |
化简可得b2+c2-a2+2bc=2b2+2bc,
∴c2=a2+b2,∴△ABC为直角三角形,
故选:B.
点评:本题考查三角形形状的判断,涉及余弦定理和降幂公式的应用,属中档题.

练习册系列答案
相关题目
下列各函数中,是偶函数且在区间(0,π)上为增函数的是( )
| A、y=cosx |
| B、y=sinx |
| C、y=-cosx |
| D、y=-cos2x |
设复数z满足iz=1+2i,则z=( )
| A、2-i | B、-2-i |
| C、-2+i | D、2+i |
曲线y=
在点(3,2)处的切线与直线ax-y+1=0垂直,则a的值为( )
| x+1 |
| x-1 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
已知lg(x+y)+lg(2x+3y)-lg3=lg4+lgx+lgy,则
的值( )
| x |
| y |
| A、3 | ||
B、3或
| ||
C、
| ||
| D、3或0 |
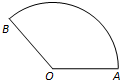 如图,扇形OAB中,OA=OB=1,
如图,扇形OAB中,OA=OB=1, |
| AB |
 |
| AB |
A、1-
| ||
B、2-
| ||
C、1-
| ||
D、
|
设p:“x,y,z中至少有一个等于1”?“(x-1)(y-1)(z-1)=0”;q:“
+|y-2|+(z-3)2=0”?“(x-1)(y-2)(z-3)=0”,那么p,q的真假是( )
| x-1 |
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
 已知函数f(x)的定义域为[-1,5],部分对应值如下表:
已知函数f(x)的定义域为[-1,5],部分对应值如下表: