题目内容
已知命题p:函数y=x3为R上的奇函数;命题q:若b2=ac,则a,b,c一定成等比数列.下列说法正确的是( )
| A、p或q为假 |
| B、p且q为真 |
| C、¬p且q为真 |
| D、¬p或q为假 |
考点:复合命题的真假
专题:简易逻辑
分析:分别判断命题p,q的真假,利用复合命题之间的关系即可得到结论.
解答:
解:∵y=x3为R上的奇函数,∴命题p为真命题,
当a=b=c=0时,满足b2=ac,则a,b,c不能构成等比数列,故命题q为假命题,
则p或q为真,p且q为假,¬p且q为假命题,¬p或q为假,
故正确的命题D,
故选:D.
当a=b=c=0时,满足b2=ac,则a,b,c不能构成等比数列,故命题q为假命题,
则p或q为真,p且q为假,¬p且q为假命题,¬p或q为假,
故正确的命题D,
故选:D.
点评:本题主要考查复合命题的真假关系的判断,判断命题p,q的真假关系是解决本题的关键.

练习册系列答案
相关题目
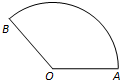 如图,扇形OAB中,OA=OB=1,
如图,扇形OAB中,OA=OB=1, |
| AB |
 |
| AB |
A、1-
| ||
B、2-
| ||
C、1-
| ||
D、
|
已知集合A={x|x2-11x+10≤0},B={y|y=lgx,x∈A},则A∪B=( )
| A、[0,1] |
| B、[1,10] |
| C、{1} |
| D、[0,10] |
 某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.
某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.| A、11 | B、13 | C、15 | D、17 |
在数列{an}中,a1=1,an+1=
(n∈N*),猜想这个数列的通项公式为( )
| 2an |
| 2+an |
| A、an=n | ||
B、an=
| ||
C、an=
| ||
D、an=
|
设p:“x,y,z中至少有一个等于1”?“(x-1)(y-1)(z-1)=0”;q:“
+|y-2|+(z-3)2=0”?“(x-1)(y-2)(z-3)=0”,那么p,q的真假是( )
| x-1 |
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
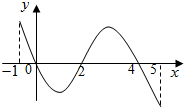 已知函数f(x)的定义域为[-1,5],部分对应值如下表:
已知函数f(x)的定义域为[-1,5],部分对应值如下表: