题目内容
2.已知常数m≠0,n≥2且n∈N,二项式(1+mx)n的展开式中,只有第6项的二项式系数最大,第三项系数是第二项系数的9倍.(1)求m、n的值;
(2)若记(1+mx)n=a0+a1(x+8)+a2(x+8)2+…+an(x+8)n,求a0-a1+a2-a3+…+(-1)nan除以6的余数.
分析 (1)利用二项式系数的性质求得n=10,再根据第三项系数是第二项系数的9倍,求得m的值.
(2)令x=-9,可得a0-a1+a2-a3+…+(-1)nan=(18-1)10,再把它按照二项式定理展开,求得它除以6的余数.
解答 解:(1)∵(1+mx)n的展开式中,只有第6项的二项式系数最大,
∴展开式共有11项,故n=10.
在(1+mx)10展开式中,第r+1项为${T_{r+1}}=C_{10}^r{(mx)^r}={m^r}C_{10}^r{x^r}(r=0,1,…,10)$,
∴第二项系数为$mC_{10}^1=10m$,第三项系数${m^2}C_{10}^2=45{m^2}$,
∴45m2=90m,∴m=2(m=0舍).
(2)在${(1+mx)^n}={a_0}+{a_1}(x+8)+{a_2}{(x+8)^2}+…+{a_k}{(x+8)^k}+…{a_n}{(x+8)^n}$中,
令x=-9,得:${a_0}-{a_1}+{a_2}-{a_3}+…+{(-1)^n}{a_n}$=(1-9m)n
=(1-9×2)10=(-17)10=1710=(18-1)10
=$C_{10}^0×{18^{10}}×{(-1)^0}+C_{10}^1×{18^9}×{(-1)^1}+…+C_{10}^9×{18^1}×{(-1)^9}+C_{10}^{10}×{18^0}×{(-1)^{10}}$
=$18[C_{10}^0×{18^9}×{(-1)^0}+C_{10}^1×{18^8}×{(-1)^1}+…+C_{10}^9×{(-1)^9}]+1$
=$6×3[C_{10}^0×{18^9}×{(-1)^0}+C_{10}^1×{18^8}×{(-1)^1}+…+C_{10}^9×{(-1)^9}]+1$,
∵$3[C_{10}^0×{18^9}×{(-1)^0}+C_{10}^1×{18^8}×{(-1)^1}+…+C_{10}^9×{(-1)^9}]∈Z$,
∴a0-a1+a2-a3+…+(-1)nan除以6的余数为1.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 0 |
| A. | 80 | B. | 120 | C. | 160 | D. | 60 |

| A. | 0或-1 | B. | 0或2 | C. | -1或2 | D. | -1或0或2 |
| A. | 5,10,15,20,25 | B. | 5,12,31,39,57 | C. | 6,16,26,36,46 | D. | 6,18,30,42,54 |
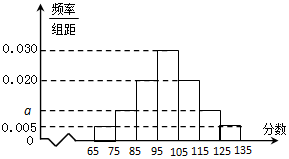 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图: