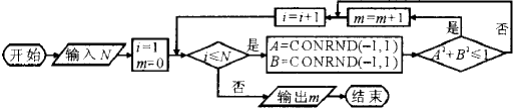
题目内容
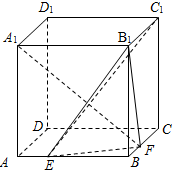 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC上的动点,且AE=BF.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC上的动点,且AE=BF.(Ⅰ)求证:A1F⊥C1E;
(Ⅱ)当三棱锥B1-BEF的体积取得最大值时,求二面角B1-EF-B的正切值.
考点:用空间向量求平面间的夹角,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:设AE=BF=x.以D为原点建立空间直角坐标系,求出相关点的坐标
(Ⅰ)通过计算
•
=0,证明A1F⊥C1E.
(Ⅱ)判断当S△BEF取得最大值时,三棱锥B1-BEF的体积取得最大值.求出平面B1EF的法向量,底面ABCD的法向量,设二面角B1-EF-B的平面角为θ,利用空间向量的数量积求出cosθ=
,然后求解二面角B1-EF-B的正切值.
(Ⅰ)通过计算
| A1F |
| C1E |
(Ⅱ)判断当S△BEF取得最大值时,三棱锥B1-BEF的体积取得最大值.求出平面B1EF的法向量,底面ABCD的法向量,设二面角B1-EF-B的平面角为θ,利用空间向量的数量积求出cosθ=
| 1 |
| 3 |
解答:
解:设AE=BF=x.以D为原点建立空间直角坐标系,得下列坐标:D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),D1(0,0,2),A1(2,0,2),B1(2,2,2),C1(0,2,2),E(2,x,0),F(2-x,2,0).
(Ⅰ)因为
=(-x,2,-2),
=(2,x-2,-2),
所以
•
=(-x,2,-2)•(2,x-2,-2)=0.
所以A1F⊥C1E.…(4分)

(Ⅱ)因为VB1-BEF=
S△BEF×BB1=
S△BEF,
所以当S△BEF取得最大值时,三棱锥B1-BEF的体积取得最大值.
因为S△BEF=(2-x)x=1-(x-1)2≤1,
所以当x=1时,即E,F分别是棱AB,BC的中点时,三棱锥B1-BEF的体积取得最大值,此时E,F坐标分别为E(2,1,0),F(1,2,0).
设平面B1EF的法向量为
=(a,b,c),
则
得
取a=2,b=2,c=-1,得
=(2,2,-1).显然底面ABCD的法向量为
=(0,0,1).
设二面角B1-EF-B的平面角为θ,由题意知θ为锐角.
因为cos<
,
>=
=-
,所以cosθ=
,于是sinθ=
.
所以tanθ=2
,即二面角B1-EF-B的正切值为2
.…(12分)
(Ⅰ)因为
| A1F |
| C1E |
所以
| A1F |
| C1E |
所以A1F⊥C1E.…(4分)

(Ⅱ)因为VB1-BEF=
| 1 |
| 3 |
| 2 |
| 3 |
所以当S△BEF取得最大值时,三棱锥B1-BEF的体积取得最大值.
因为S△BEF=(2-x)x=1-(x-1)2≤1,
所以当x=1时,即E,F分别是棱AB,BC的中点时,三棱锥B1-BEF的体积取得最大值,此时E,F坐标分别为E(2,1,0),F(1,2,0).
设平面B1EF的法向量为
| m |
则
|
|
取a=2,b=2,c=-1,得
| m |
| n |
设二面角B1-EF-B的平面角为θ,由题意知θ为锐角.
因为cos<
| m |
| n |
| ||||
|
|
| 1 |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
所以tanθ=2
| 2 |
| 2 |
点评:本题考查空间向量在立体几何值的应用,直线与直线的垂直,二面角的求法,考查空间想象能力以及计算能力.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
条件语句的一般形式如图所示,其中B表示的是( )


| A、条件 |
| B、条件语句 |
| C、满足条件时执行的内容 |
| D、不满足条件时执行的内容 |
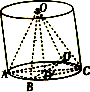 在一个圆柱中挖去一个内接正四棱锥O-ABCD(顶点是上面底面积圆的圆心O,底面是下底面的内接正方形),得到如图所示的几何体,已知圆柱底面直径为4
在一个圆柱中挖去一个内接正四棱锥O-ABCD(顶点是上面底面积圆的圆心O,底面是下底面的内接正方形),得到如图所示的几何体,已知圆柱底面直径为4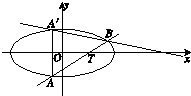 如图所示,已知椭圆C:
如图所示,已知椭圆C: