题目内容
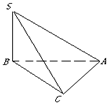 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,SB=a,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,SB=a,则以下结论中:①异面直线SB与AC所成的角为90°;
②直线SB⊥平面ABC;
③面SBC⊥面SAC;
④三棱锥S-ABC外接球的表面积为πa2.
正确的为
考点:命题的真假判断与应用
专题:空间位置关系与距离,简易逻辑
分析:由题目中的条件可以证得,三棱锥的一个侧棱SB⊥平面ABC,面SBC⊥AC,由此易判断得①②③都是正确的;再由题意可得SA为三棱锥S-ABC外接球的直径,解直角三角形求得SA后代入球的表面积公式判断.
解答:
解:由题意三棱锥S-ABC中,∠SBA=∠SCA=90°,知SB⊥BA,SC⊥CA,
又△ABC是斜边AB=a的等腰直角三角形可得AC⊥BC,又BC∩SB=B,故有AC⊥面SBC,故有SB⊥AC,故①正确,
由此可以得到SB⊥平面ABC,故②正确,
再有AC?面SAC得面SBC⊥面SAC,故③正确,
△SAB是以SA为斜边的直角三角形,△SCA是以SA为斜边的直角三角形,∴SA为三棱锥S-ABC外接球的直径,
∵SB=a,△ABC是斜边AB=a的等腰直角三角形,∴AB=
a,SA=
=
a,
∴三棱锥S-ABC外接球的表面积为44π×(
)2=3πa2,故④错误.
故答案为:①②③.
又△ABC是斜边AB=a的等腰直角三角形可得AC⊥BC,又BC∩SB=B,故有AC⊥面SBC,故有SB⊥AC,故①正确,
由此可以得到SB⊥平面ABC,故②正确,
再有AC?面SAC得面SBC⊥面SAC,故③正确,
△SAB是以SA为斜边的直角三角形,△SCA是以SA为斜边的直角三角形,∴SA为三棱锥S-ABC外接球的直径,
∵SB=a,△ABC是斜边AB=a的等腰直角三角形,∴AB=
| 2 |
a2+(
|
| 3 |
∴三棱锥S-ABC外接球的表面积为44π×(
| ||
| 2 |
故答案为:①②③.
点评:本题考查了命题的真假判断与应用,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
某几何体的三视图(单位:cm)如图所示,则该几何体的体积为:( )
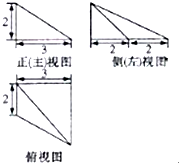

| A、2cm2 | ||
B、
| ||
C、
| ||
| D、6cm2 |
条件语句的一般形式如图所示,其中B表示的是( )


| A、条件 |
| B、条件语句 |
| C、满足条件时执行的内容 |
| D、不满足条件时执行的内容 |
 已知函数f(x)=-4x2+4ax-4a-a2.
已知函数f(x)=-4x2+4ax-4a-a2.