题目内容
已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合,直线l的极坐标方程为:ρsin(θ-
)=
,曲线C的参数方程为:
(α为参数).
(I)写出直线l的直角坐标方程;
(Ⅱ)求曲线C上的点到直线l的距离的最大值.
| π |
| 6 |
| 1 |
| 2 |
|
(I)写出直线l的直角坐标方程;
(Ⅱ)求曲线C上的点到直线l的距离的最大值.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)首先,将直线的极坐标方程中消去参数,化为直角坐标方程即可;
(2)首先,化简曲线C的参数方程,然后,根据直线与圆的位置关系进行转化求解.
(2)首先,化简曲线C的参数方程,然后,根据直线与圆的位置关系进行转化求解.
解答:
解:(1)∵直线l的极坐标方程为:ρsin(θ-
)=
,
∴ρ(
sinθ-
cosθ)=
,
∴
y-
x=
,
∴x-
y+1=0.
(2)根据曲线C的参数方程为:
(α为参数).
得
(x-2)2+y2=4,
它表示一个以(2,0)为圆心,以2为半径的圆,
圆心到直线的距离为:
d=
,
∴曲线C上的点到直线l的距离的最大值
+2=
.
| π |
| 6 |
| 1 |
| 2 |
∴ρ(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴x-
| 3 |
(2)根据曲线C的参数方程为:
|
得
(x-2)2+y2=4,
它表示一个以(2,0)为圆心,以2为半径的圆,
圆心到直线的距离为:
d=
| 3 |
| 2 |
∴曲线C上的点到直线l的距离的最大值
| 3 |
| 2 |
| 7 |
| 2 |
点评:本题重点考查了直线的极坐标方程、曲线的参数方程、及其之间的互化等知识,属于中档题.

练习册系列答案
相关题目
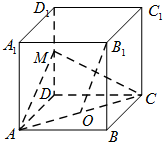 在正方体ABCD-A1B1C1D1中,M,O分别为DD1,AC的中点,AB=2.
在正方体ABCD-A1B1C1D1中,M,O分别为DD1,AC的中点,AB=2.