题目内容
16.设数列{an}中,若${a_{n+1}}={a_n}+{a_{n+2}}(n∈{N^*})$,则称数列{an}为“凸数列”.已知数列{bn}为“凸数列”,且b1=1,b2=-2,则数列{bn}的前2016项的和为( )| A. | 0 | B. | -2 | C. | -4 | D. | 2 |
分析 数列{bn}为“凸数列”,bn+1=bn+bn+2,b1=1,b2=-2,可得:b3=-3,b4,b5,b6,b7,b8,…,bn+6=bn.即可得出.
解答 解:∵数列{bn}为“凸数列”,
∴bn+1=bn+bn+2,
∵b1=1,b2=-2,
∴-2=1+b3,
解得b3=-3,
同理可得:b4=-1,b5=2,b6=3,b7=1,b8=-2…,
∴bn+6=bn.
则数列{bn}的前2016项的和=336(b1+b2+…+b6)
=336(1-2-3-1+2+3)=0,
故选:A.
点评 本题考查了递推关系的应用、新定义、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.将函数y=sin2x的图象向左$\frac{π}{6}$平移个单位,向上平移1个单位,得到的函数解析式为( )
| A. | y=sin(2x+$\frac{π}{3}$)+1 | B. | y=sin(2x-$\frac{π}{3}$)+1 | C. | y=sin(2x+$\frac{π}{6}$)+1 | D. | y=sin(2x-$\frac{π}{6}$)+1 |
5.如图是函数f(x)=sin(x+φ)一个周期内的图象,则φ可能等于( )
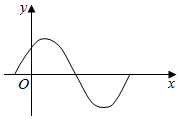

| A. | $\frac{5π}{6}$ | B. | $\frac{π}{2}$ | C. | $-\frac{π}{6}$ | D. | $\frac{π}{6}$ |