题目内容
15.复数$\frac{2a+i}{1-2i}{i^{2015}}(i$是虚数单位)为纯虚数,则实数a的值为$-\frac{1}{4}$.分析 利用复数代数形式的乘除运算化简复数为a+bi(a,b∈R)的形式,然后由复数的实部等于零且虚部不等于0求出实数a的值即可.
解答 解:$\frac{2a+i}{1-2i}{i}^{2015}$=$\frac{(2a+i)(1+2i)}{(1-2i)(1+2i)}{i}^{2015}$=$\frac{2a-2+(4a+1)i}{5}({i}^{2})^{1007}•i$=$\frac{4a+1}{5}-\frac{2a-2}{5}i$,
∵复数$\frac{2a+i}{1-2i}{i^{2015}}(i$是虚数单位)为纯虚数,
∴$\left\{\begin{array}{l}{\frac{4a+1}{5}=0}\\{-\frac{2a-2}{5}≠0}\end{array}\right.$,解得:a=$-\frac{1}{4}$.
故答案为:$-\frac{1}{4}$.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.函数y=2x+log2(x+1)在区间[0,1]上的最大值和最小值之和为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
5.如图是函数f(x)=sin(x+φ)一个周期内的图象,则φ可能等于( )
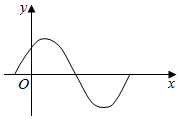

| A. | $\frac{5π}{6}$ | B. | $\frac{π}{2}$ | C. | $-\frac{π}{6}$ | D. | $\frac{π}{6}$ |
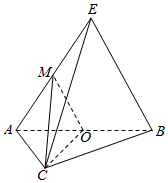 如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.
如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.