题目内容
20.设a=${∫}_{0}^{π}$(cosx-sinx)dx,则二项式(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6的展开式中含x2项的系数为192.分析 根据微积分基本定理首先求出a的值,然后再根据二项式的通项公式求出r的值,问题得以解决.
解答 解:由于a=${∫}_{0}^{π}$(cosx-sinx)dx=(sinx+cosx)|${\;}_{0}^{π}$=-1-1=-2,
∴(-2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6=(2$\sqrt{x}$+$\frac{1}{\sqrt{x}}$)6 的通项公式为 Tr+1=26-rC6r•x3-r,
令3-r=2,求得r=1,故含x2项的系数为26-1C61=192.
故答案为:192
点评 本题主要考查定积分、二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
相关题目
10.若cos($\frac{π}{8}$-α)=$\frac{1}{6}$,则cos($\frac{3π}{4}$+2α)的值为( )
| A. | $\frac{17}{18}$ | B. | -$\frac{17}{18}$ | C. | $\frac{18}{19}$ | D. | -$\frac{18}{19}$ |
8.等差数列{an}的前n项和为Sn,且S5=15,a2=5,则公差d等于( )
| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
5.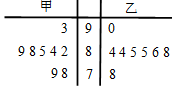 某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
 某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )| A. | 甲、乙生产的零件尺寸的中位数相等 | |
| B. | 甲、乙生产的零件质量相当 | |
| C. | 甲生产的零件质量比乙生产的零件质量好 | |
| D. | 乙生产的零件质量比甲生产的零件质量好 |
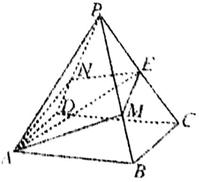 如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC上的点,过AE作平面分别与棱PB、PD交于M、N两点,且$\frac{PM}{PB}$=$\frac{PN}{PD}$=$\frac{2}{3}$.
如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC上的点,过AE作平面分别与棱PB、PD交于M、N两点,且$\frac{PM}{PB}$=$\frac{PN}{PD}$=$\frac{2}{3}$.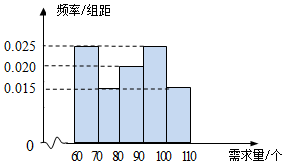 在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.
在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.