题目内容
10.若cos($\frac{π}{8}$-α)=$\frac{1}{6}$,则cos($\frac{3π}{4}$+2α)的值为( )| A. | $\frac{17}{18}$ | B. | -$\frac{17}{18}$ | C. | $\frac{18}{19}$ | D. | -$\frac{18}{19}$ |
分析 利用二倍角公式求出cos($\frac{π}{4}$-2α)的值,再利用诱导公式求出cos($\frac{3π}{4}$+2α)的值.
解答 解:∵cos($\frac{π}{8}$-α)=$\frac{1}{6}$,
∴cos($\frac{π}{4}$-2α)=2cos2($\frac{π}{8}$-α)-1
=2×${(\frac{1}{6})}^{2}$-1
=-$\frac{17}{18}$,
∴cos($\frac{3π}{4}$+2α)=cos[π-($\frac{π}{4}$-2α)]
=-cos($\frac{π}{4}$-2α)
=$\frac{17}{18}$.
故选:A.
点评 本题考查了余弦二倍角公式与诱导公式的应用问题,是基础题.

练习册系列答案
相关题目
18.已知数列{an}满足an+1-an=2,a1=-5,则|a1|+|a2|+…+|a6|=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 30 |
5.设集合A={x|x2-16>0},B={x|-2<x≤6},则A∩B等于( )
| A. | (-2,4) | B. | (4,6] | C. | (-4,6) | D. | (-4,-2) |
2.复数(2+i)i的共轭复数的虚部是( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
19.若点P为抛物线$C:{x^2}=\frac{1}{2}y$上的动点,F为抛物线C的焦点,则|PF|的最小值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
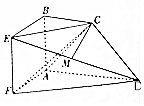 如图,已知四边形ABEF于ABCD分别为正方形和直角梯形,平面ABEF⊥平面ABCD,AB=BC=$\frac{1}{2}$AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.
如图,已知四边形ABEF于ABCD分别为正方形和直角梯形,平面ABEF⊥平面ABCD,AB=BC=$\frac{1}{2}$AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.