题目内容
15.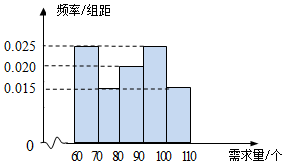 在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.
在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.(Ⅰ)求T关于x的函数解析式;
(Ⅱ)根据直方图估计利润T不少于100元的概率;
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量x∈[60,70),则取x=65,且x=65的概率等于需求量落入[60,70)的频率),求T的分布列和数学期望.
分析 (Ⅰ)由题意,当60≤X≤90时,求出利润T,当90<X≤110时,求出利润T,由此能求出T关于x的函数解析式.
(Ⅱ)由题意,设利润T不少于100元为事件A,利润T不少于100元时,即70≤X≤110,由此利用对立事件概率计算公式能求出T的分布列和数学期望.
(III)由题意,利润T的取值可为:80,120,160,180,分别求出相应的概率,由此能求出利润的数学期望E(T).
解答 解:(Ⅰ)由题意,当60≤X≤90时,利润T=5X+1×(90-X)-3×90=4X-180,
当90<X≤110时,利润T=5×90-3×90=180,
即T关于x的函数解析式T=$\left\{\begin{array}{l}{4X-180,(60≤X≤90)}\\{180,(90<X≤110)}\end{array}\right.$.…(4分)
(Ⅱ)由题意,设利润T不少于100元为事件A,
由(Ⅰ)知,利润T不少于100元时,即4X-180≥100,
∴X≥70,即70≤X≤110,
由直方图可知,当70≤X≤110时,
所求概率为:
P(A)=1-P($\overline{A}$)=1-0.025×(70-60)=0.75.…(7分)
( III)由题意,由于4×65-180=80,4×75-180=120,
4×85-180=160,
故利润T的取值可为:80,120,160,180,
且P(T=80)=0.25,P(T=120)=0.15,P(T=160)=0.2,P(T=180)=0.4,…(9分)
故T的分布列为:
| T | 80 | 120 | 160 | 180 |
| P | 0.25 | 0.15 | 0.2 | 0.4 |
E(T)=80×0.25+120×0.15+160×0.20+180×0.40=142.…(12分)
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,考查推理论证能力、运算求解能力、空间思维能力,考查数形结合思想、转化化归思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.设集合A={x|x2-16>0},B={x|-2<x≤6},则A∩B等于( )
| A. | (-2,4) | B. | (4,6] | C. | (-4,6) | D. | (-4,-2) |
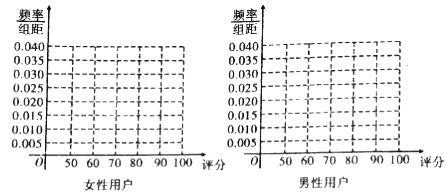
6.某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望.
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望.

10.将函数$y=2sin(\frac{2}{3}x+\frac{3π}{4})$图象上所有点的横坐标缩短为原来的$\frac{1}{3}$,纵坐标不变,再向右平移$\frac{π}{8}$个单位长度,得到函数y=g(x)的图象,则下列说法正确的是( )
| A. | 函数g(x)的一条对称轴是$x=\frac{π}{4}$ | B. | 函数g(x)的一个对称中心是$(\frac{π}{2},0)$ | ||
| C. | 函数g(x)的一条对称轴是$x=\frac{π}{2}$ | D. | 函数g(x)的一个对称中心是$(\frac{π}{8},0)$ |
5.若复数z满足$\overline{z}$-|z|=-1-3i,其中i为虚数单位,则z=( )
| A. | 4+3i | B. | 3+4i | C. | -5+3i | D. | 4-3i |