Question

正四棱锥底面边长为4cm，侧面和底面成60°的二面角，则这个棱锥的侧面积是

 

cm²．

Answer 1

考点：旋转体（圆柱、圆锥、圆台）

专题：空间位置关系与距离

分析：画出正四棱锥图形，根据题意，侧面与底面成60°的二面角，求出棱锥的斜高，即可求出棱锥的侧面积．

解答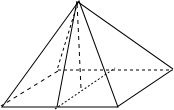： 解：由题意作出图形如图：
因为侧面与底面成60°的二面角，
所以棱锥的斜高为：

2

cos60°

=4，
则这个棱锥的侧面积S=4×

1

2

×4×4=32（cm²）．
故答案为：32．

点评：本题考查棱柱、棱锥、棱台的侧面积和表面积，棱锥的结构特征，二面角及其度量，还考查计算能力，是基础题．