题目内容
13.平面α过正方体ABCD-A1B1C1D1的面对角线$AB_1^{\;}$,且平面α⊥平面C1BD,平面α∩平面ADD1A1=AS,则∠A1AS的正切值为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
分析 推导出A1C⊥BD,A1C⊥BC1,从而A1C⊥平面C1BD,以AA1为侧棱补作一个正方体AEFG-A1PQS,使得侧面AGRA1与平面ADD1A1共面,连结AQ,则AQ∥CA1,连结QB1,交A1R于S,则平面AQB1就是平面α,且AS为所求作,由此能求出结果.
解答 解:正方体ABCD-A1B1C1D1中,BD⊥AC,BD⊥AA1,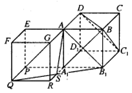
∵AC∩AA1=A,∴BD⊥平面AA1C,∴A1C⊥BD,
同理,得A1C⊥BC1,
∵BD∩BC1=B,∴A1C⊥平面C1BD,
如图,以AA1为侧棱补作一个正方体AEFG-A1PQS,
使得侧面AGRA1与平面ADD1A1共面,
连结AQ,则AQ∥CA1,连结QB1,交A1R于S,则平面AQB1就是平面α,且AS为所求作,
∵AQ∥CA1,∴AQ⊥平面C1BD,
∵AQ?平面α,∴平面α⊥平面C1BD,
∴tan∠A1AS=$\frac{{A}_{1}S}{A{A}_{1}}$=$\frac{1}{2}$.
故选:D.
点评 本题考查平角的正切值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查数形结合思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{3}$)=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{3}$)=( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{3}$)=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{3}$)=( )| A. | $-\frac{1}{2}$ | B. | -1 | C. | 1 | D. | $\sqrt{2}$ |
2.将函数y=sin(2x+$\frac{π}{6}$)图象上的点M(θ,$\frac{\sqrt{3}}{2}$)(0<θ<$\frac{π}{4}$)向右平移t(t>0)个单位长度得到点M′.若M′位于函数y=sin2x的图象上,则( )
| A. | θ=$\frac{π}{12}$,t的最小值为$\frac{π}{12}$ | B. | θ=$\frac{π}{12}$,t的最小值为$\frac{π}{6}$ | ||
| C. | θ=$\frac{π}{6}$,t的最小值为$\frac{π}{6}$ | D. | θ=$\frac{π}{6}$,t的最小值为$\frac{π}{12}$ |
3.若点P是曲线$y=\frac{3}{2}{x^2}-2lnx$上任意一点,则点P到直线$y=x-\frac{5}{2}$的距离的最小值为( )
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{5}$ |
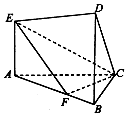 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB