题目内容
已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f(
)|对x∈R恒成立且f(
)<f(π),则下列结论正确的是( )
| π |
| 6 |
| π |
| 2 |
A、f(
| ||||
B、f(
| ||||
| C、f(x)是奇函数 | ||||
D、[0,
|
考点:正弦函数的单调性
专题:三角函数的图像与性质
分析:利用正弦函数的对称性与单调性,可求得φ=2kπ+
(k∈Z),于是得到f(x)=sin(2x+
),再对A、B、C、D四个选项逐一分析判断即可.
| π |
| 6 |
| π |
| 6 |
解答:
解:∵f(x)=sin(2x+φ),f(x)≤|f(
)|对x∈R恒成立,
∴x=
为函数f(x)的一条对称轴,
∴2×
+φ=kπ+
(k∈Z);
∴φ=kπ+
(k∈Z);
又f(
)<f(π),∴sin(π+φ)<sin(2π+φ),∴sinφ>0,
∴φ=2kπ+
(k∈Z),
∴f(x)=sin(2x+
);
对于A,∵f(
)=sin(
+
)=0,故A错误;
对于B,f(
)=sin(
+
)=-sin(
+
)<sin(
+
)=f(
),故B错误;
对于C,f(0)=sin
=
≠0,故f(x)不是奇函数,故C错误;
对于D,当x∈[0,
]时,(2x+
)∈[
,
],f(x)=sin(2x+
)为增函数,故D正确.
故选:D.
| π |
| 6 |
∴x=
| π |
| 6 |
∴2×
| π |
| 6 |
| π |
| 2 |
∴φ=kπ+
| π |
| 6 |
又f(
| π |
| 2 |
∴φ=2kπ+
| π |
| 6 |
∴f(x)=sin(2x+
| π |
| 6 |
对于A,∵f(
| 11π |
| 12 |
| 11π |
| 6 |
| π |
| 6 |
对于B,f(
| 7π |
| 10 |
| 7π |
| 5 |
| π |
| 6 |
| 2π |
| 5 |
| π |
| 6 |
| 2π |
| 5 |
| π |
| 6 |
| π |
| 5 |
对于C,f(0)=sin
| π |
| 6 |
| 1 |
| 2 |
对于D,当x∈[0,
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
故选:D.
点评:本题考查正弦函数的图象与性质,着重考查正弦函数的对称性、奇偶性与单调性的综合判断,考查分析、运算能力,属于中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
若实数x,y满足
,则z=3x+2y的值域是( )
|
| A、[0,6] |
| B、[1,9] |
| C、[2,8] |
| D、[3,7] |
国家征收个人所得税是分段计算的,总收入不超过3500的免征个人所得税,超过3500元的部分为全月应纳税额,税率表为:
某人某月总收入为6000元,则他当月应缴纳的税额为( )
| 全月应纳税额 | 税率 |
| 不超过1500元的部分 | 3% |
| 超过1500元至4500元的部分 | 10% |
| 超过4500元至9000元的部分 | 20% |
| A、1200元 | B、2500 |
| C、145元 | D、100元 |
函数y=logax (0<a<1)的图象大致是( )
A、 |
B、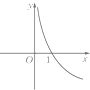 |
C、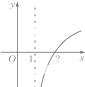 |
D、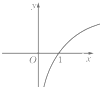 |
已知等比数列{an}中,
=2,a4=8,则a6=( )
| a2+a3 |
| a1+a2 |
| A、31 | B、32 | C、63 | D、64 |
 已知正四棱锥(底面是正方形,顶点在底面的投影是底面的中心)P-ABCD如图.
已知正四棱锥(底面是正方形,顶点在底面的投影是底面的中心)P-ABCD如图.