题目内容
1．若双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$的两条渐近线恰好是曲线$y=a{x^2}+\frac{1}{3}$的两条切线，则a的值为$\frac{1}{3}$．分析 先求出双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$的两条渐近线方程，再与抛物线方程联立，利用相切找到对应的判别式为0即可求出a的值．
解答 解：由题得，双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$的两条渐近线方程为y=±$\frac{2}{3}$x，
又因为是曲线$y=a{x^2}+\frac{1}{3}$的两条切线，
所以联立可得⇒ax2±$\frac{2}{3}$x+$\frac{1}{3}$=0对应△=$\frac{4}{9}$-4×$\frac{1}{3}$a=0
解得a=$\frac{1}{3}$，
故答案为：$\frac{1}{3}$．
点评 本题涉及到双曲线的两条渐近线方程的求法，在求双曲线的两条渐近线方程时，一定要先看焦点在X轴上还是焦点在Y轴上．
练习册系列答案
名校课堂系列答案
相关题目
11．点M是抛物线x2=2py（p＞0）的对称轴与准线的交点，点F为抛物线的焦点，P在抛物线上，在△PFM中，sin∠PFM=λsin∠PMF，则λ的最大值为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | 1 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
13．已知函数y=sin（2x+φ）+1的图象关于直线$x=-\frac{π}{8}$对称，则φ的可能取值是（ ）
| A． | $\frac{3π}{4}$ | B． | $-\frac{3π}{4}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{2}$ |
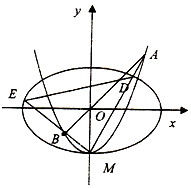如图，椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，x轴被曲线C2：y=x2-b截得的线段长等于C1的短轴长，C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A、B，直线MA，MB分别与C1相交于点D、E．