Question

11．点M是抛物线x²=2py（p＞0）的对称轴与准线的交点，点F为抛物线的焦点，P在抛物线上，在△PFM中，sin∠PFM=λsin∠PMF，则λ的最大值为（　　）

• A． $\frac{{\sqrt{2}}}{2}$
• B． 1
• C． $\sqrt{2}$
• D． $\sqrt{3}$

Answer 1

分析 由正弦定理求得丨PM丨=λ丨PF丨，根据抛物线的定义，则$\frac{1}{λ}$=$\frac{丨PB丨}{丨PM丨}$，sinα=$\frac{1}{λ}$，则λ取得最大值时，sinα最小，此时直线PM与抛物线相切，将直线方程代入抛物线方程，△=0，求得k的值，即可求得λ的最大值．

解答 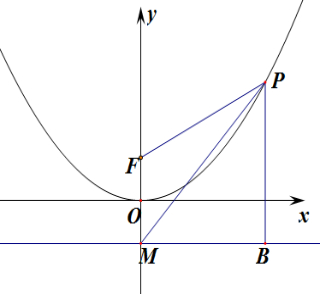解：过P作准线的垂线，垂足为B，则由抛物线的定义可得|PF|=|PB|，由sin∠PFM=λsin∠PMF，
则△PFM中由正弦定理可知：则丨PM丨=λ丨PF丨，
∴|PM|=λ|PB|
∴$\frac{1}{λ}$=$\frac{丨PB丨}{丨PM丨}$，
设PM的倾斜角为α，则sinα=$\frac{1}{λ}$，
当λ取得最大值时，sinα最小，此时直线PM与抛物线相切，
设直线PM的方程为y=kx-$\frac{p}{2}$，则$\left\{\begin{array}{l}{{x}^{2}=2py}\\{y=kx-\frac{p}{2}}\end{array}\right.$，
即x²-2pkx+p²=0，
∴△=4p²k²-4p²=0，
∴k=±1，即tanα=±1，
则sinα=$\frac{\sqrt{2}}{2}$，
则λ的最大值为$\frac{1}{sinα}$=$\sqrt{2}$，
故选：C．

点评 本题考查抛物线的标准方程，直线与抛物线的位置关系，考查正弦定理，考查直线与抛物线相切，考查计算能力，属于中档题．