题目内容
在△ABC中，已知asinA=bsinB，那么△ABC的形状 三角形．
考点：三角形的形状判断
专题：解三角形
分析：由条件利用正弦定理可得sinA=sinB，故有a=b，可得△ABC为等腰三角形．
解答：
解：∵△ABC中，已知asinA=bsinB，∴由正弦定理可得 sinAsinA=sinBsinB，
∴sinA=sinB，∴a=b，故△ABC为等腰三角形，
故答案为：等腰．
∴sinA=sinB，∴a=b，故△ABC为等腰三角形，
故答案为：等腰．
点评：本题主要考查正弦定理的应用，属于基础题．
练习册系列答案
优加精卷系列答案
相关题目
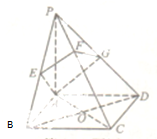如图，四棱锥P-ABCD中，底面ABCD是正方形，PA⊥平面ABCD，过A点的截面AEFG分别交PB，PC，PD于点E，F，G，且PB⊥AE，PD⊥AG．下列结论正确的是设z=3-4i，则复数的虚部是（ ）
| A、3 | B、4 | C、-4 | D、-4i |