题目内容
若f(x)=2xf′(1)+x2,则f′(0)= .
考点:导数的运算
专题:导数的概念及应用
分析:求函数的导数,令x=1,先求出f′(1)的值,即可得到结论.
解答:
解:∵f(x)=x2+2x f′(1),
∴f′(x)=2x+2f′(1),
令x=1,则f′(1)=2+2f′(1)
即f′(1)=-2,
则f′(x)=2x-4,
则f′(0)=-4,
故答案为:-4
∴f′(x)=2x+2f′(1),
令x=1,则f′(1)=2+2f′(1)
即f′(1)=-2,
则f′(x)=2x-4,
则f′(0)=-4,
故答案为:-4
点评:本题主要考查导数的计算,根据导数公式是解决本题的关键.

练习册系列答案
相关题目
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若α∥β,m?α,n?β,则m∥n |
| C、若α⊥β=m,n?α,则n⊥β |
| D、若m⊥α,m∥n,n?β,则α⊥β |
下列命题正确的是( )
| A、圆心和圆上两点可以确定一个平面 |
| B、已知a、b、c、d是四条直线,若a∥b,b∥c,c∥d,则a∥d |
| C、两条直线a,b没有公共点,那么a与b是异面直线 |
| D、若a,b是两条直线,α,β是两个平面,且a?α,b?β,则a,b是异面直线 |
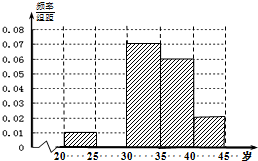 对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得:
对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得: 如图,已知Rt△ABC的两条直角边AC、BC的长分别为4cm、3cm,以AC为直径作圆与斜边AB交于点D,则BD的长为
如图,已知Rt△ABC的两条直角边AC、BC的长分别为4cm、3cm,以AC为直径作圆与斜边AB交于点D,则BD的长为