题目内容
给出下列四个命题:
①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;
②a、b、c是空间中的三条直线,a∥b的充要条件是a⊥c且b⊥c;
③命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题;
④对任意实数x,有f(-x)=f(x),且当x>0时,f′(x)>0,则当x<0时,f′(x)<0.
其中的真命题是 .(写出所有真命题的编号)
①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;
②a、b、c是空间中的三条直线,a∥b的充要条件是a⊥c且b⊥c;
③命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题;
④对任意实数x,有f(-x)=f(x),且当x>0时,f′(x)>0,则当x<0时,f′(x)<0.
其中的真命题是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用命题的否定即可判断出;
②由a⊥c且b⊥c可得a∥b或相交或为异面直线,另一方面由a∥b,推不出a⊥c,b⊥c,即可判断出;
③在△ABC中,A>B?a>b,由正弦定理可得:
=
,可得sinA>sinB.
④利用偶函数的性质即可得出.
②由a⊥c且b⊥c可得a∥b或相交或为异面直线,另一方面由a∥b,推不出a⊥c,b⊥c,即可判断出;
③在△ABC中,A>B?a>b,由正弦定理可得:
| a |
| sinA |
| b |
| sinB |
④利用偶函数的性质即可得出.
解答:
解:①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”,正确;
②a、b、c是空间中的三条直线,由a⊥c且b⊥c可得a∥b或相交或为异面直线,
由a∥b,推不出a⊥c,b⊥c,因此“a⊥c且b⊥c”是a∥b的既不充分也不必要条件,因此②不正确;
③在△ABC中,由A>B?a>b,由正弦定理可得:
=
,
因此sinA>sinB.可知逆命题为真命题,因此不正确;
④对任意实数x,有f(-x)=f(x),可知函数f(x)是偶函数.
由当x>0时,f′(x)>0,则当x<0时,f′(x)<0.正确.
综上可知:只有①④正确.
故答案为:①④.
②a、b、c是空间中的三条直线,由a⊥c且b⊥c可得a∥b或相交或为异面直线,
由a∥b,推不出a⊥c,b⊥c,因此“a⊥c且b⊥c”是a∥b的既不充分也不必要条件,因此②不正确;
③在△ABC中,由A>B?a>b,由正弦定理可得:
| a |
| sinA |
| b |
| sinB |
因此sinA>sinB.可知逆命题为真命题,因此不正确;
④对任意实数x,有f(-x)=f(x),可知函数f(x)是偶函数.
由当x>0时,f′(x)>0,则当x<0时,f′(x)<0.正确.
综上可知:只有①④正确.
故答案为:①④.
点评:本题综合考查了空间中的线线位置关系、三角形的边角关系、函数的奇偶性单调性、简易逻辑等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
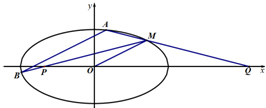 如图,已知离心率为
如图,已知离心率为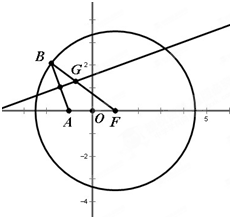 已知:定点A(-1,0),点B是⊙F:(x-1)2+y2=8(F为圆心)上的动点,线段AB的垂直平分线交BF于点G,记点G的轨迹为曲线E.
已知:定点A(-1,0),点B是⊙F:(x-1)2+y2=8(F为圆心)上的动点,线段AB的垂直平分线交BF于点G,记点G的轨迹为曲线E.