题目内容
15.对于函数f(x)和实数M,若存在m,n∈N*,使f(m)+f(m+1)+f(m+2)+…+f(m+n)=M成立,则称(m,n)为函数f(x)关于M的一个“生长点”.若(1,2)为函数$f(x)=cos({\frac{π}{2}x+\frac{π}{3}})$关于M的一个“生长点”,则M=-$\frac{1}{2}$.分析 由(1,2)为函数$f(x)=cos({\frac{π}{2}x+\frac{π}{3}})$关于M的一个“生长点”,得到M=cos($\frac{π}{2}+\frac{π}{3}$)+cos($π+\frac{π}{3}$)+cos($\frac{3π}{2}+\frac{π}{3}$),由此利用诱导公式能求出结果.
解答 解:∵(1,2)为函数$f(x)=cos({\frac{π}{2}x+\frac{π}{3}})$关于M的一个“生长点”,
∴M=f(1)+f(1+1)+f(1+2)
=cos($\frac{π}{2}+\frac{π}{3}$)+cos($π+\frac{π}{3}$)+cos($\frac{3π}{2}+\frac{π}{3}$)
=-sin$\frac{π}{3}$-cos$\frac{π}{3}$+sin$\frac{π}{3}$
=-cos$\frac{π}{3}$=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质、诱导公式的合理运用.

练习册系列答案
相关题目
6.某程序框图如图所示,若该程序运行后输出的值是10,则a的值是( )
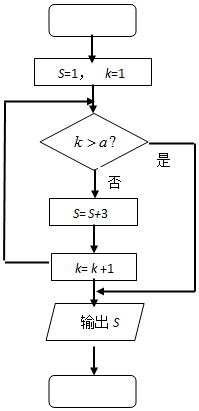

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20.一扇形的圆心角为60°,所在圆的半径为6,则它的面积是( )
| A. | 6π | B. | 3π | C. | 12π | D. | 9π |