题目内容
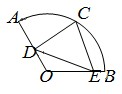
与直线x+y-2=0和圆（x-6）2+（y-6）2=18都相切的半径最小的圆的标准方程是 ．
考点：圆的标准方程,圆的切线方程
专题：直线与圆
分析：由已知条件推导出与直线x+y-2=0和圆（x-6）2+（y-6）2=18都相切的半径最小的圆的圆心在过C与x+y-2=0垂直的直线l上，由此能求出圆的方程．
解答：
解：圆：（x-6）2+（y-6）2=18的圆心C（6，6），半径r=3
，
圆心C（6，6）到x+y-2=0的距离：d=
=5
，
与直线x+y-2=0和圆（x-6）2+（y-6）2=18都相切的半径最小的圆的圆心在过C与x+y-2=0垂直的直线l上，
所求圆的半径R=
(5
-3
)=
，
直线l：y-6=x-6，即y=x，
设所求圆方程为：（x-a）2+（y-a）2=2，
解方程组：
，得x+y-2=0与l的交点（1，1），
解方程：（a-1）2+（a-1）2=2，得a=2，或a=0不符合已知条件，舍去．
∴所求圆方程为：（x-2）2+（y-2）2=2．
故答案为：（x-2）2+（y-2）2=2．
| 2 |
圆心C（6，6）到x+y-2=0的距离：d=
| |6+6-2| | ||
|
| 2 |
与直线x+y-2=0和圆（x-6）2+（y-6）2=18都相切的半径最小的圆的圆心在过C与x+y-2=0垂直的直线l上，
所求圆的半径R=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
直线l：y-6=x-6，即y=x，
设所求圆方程为：（x-a）2+（y-a）2=2，
解方程组：
|
解方程：（a-1）2+（a-1）2=2，得a=2，或a=0不符合已知条件，舍去．
∴所求圆方程为：（x-2）2+（y-2）2=2．
故答案为：（x-2）2+（y-2）2=2．
点评：本题考查圆的方程的求法，是中档题，解题时要认真审题，注意点到直线的距离公式的灵活运用．
练习册系列答案
相关题目
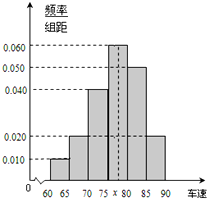2014年“五一”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/t）分成六段：[60，65），[65，70），[70，75），[75，80），[80，85），[85，90）后得到如图所示的频率分布直方图．若从车速在[60，70）的车辆中任抽取2辆，则车速在[65，70）的车辆至少有一辆的概率
