题目内容
在△ABC中，内角A、B、C的对边分别为a、b、c，已知a、b、c成等比数列，且cosB=
．
（Ⅰ）求
+
的值；
（Ⅱ）设
•
=
，求a、c的值．
| 3 |
| 4 |
（Ⅰ）求
| 1 |
| tanA |
| 1 |
| tanC |
（Ⅱ）设
| BA |
| BC |
| 3 |
| 2 |
考点：平面向量数量积的运算,同角三角函数基本关系的运用
专题：平面向量及应用
分析：（Ⅰ）由cosB=
，B∈（0，π）．可得sinB=
．由a、b、c成等比数列，可得b2=ac，再利用正弦定理可得sinAsinC=sin2B．于是可得
+
=
+
=
=
；
（Ⅱ）设
•
=
，则accosB=
，可得ac=2．再利用余弦定理可得：b2=a2+c2-2accosB化简整理，联立即可得出．
| 3 |
| 4 |
| 1-cos2B |
| 1 |
| tanA |
| 1 |
| tanC |
| cosA |
| sinA |
| cosC |
| sinC |
| sin(A+C) |
| sinAsinC |
| sinB |
| sin2B |
（Ⅱ）设
| BA |
| BC |
| 3 |
| 2 |
| 3 |
| 2 |
解答：
解：（Ⅰ）由cosB=
，B∈（0，π）．
∴sinB=
=
．
∵a、b、c成等比数列，∴b2=ac，
由正弦定理可得sinAsinC=sin2B．
∴
+
=
+
=
=
=
=
；
（Ⅱ）设
•
=
，则accosB=
，∴
ac=
，化为ac=2．
由余弦定理可得：2=ac=b2=a2+c2-2accosB=a2+c2-2ac×
，化为a2+c2=5．
联立
，解得
或
．
即a=2，c=1，或a=1，c=2．
| 3 |
| 4 |
∴sinB=
| 1-cos2B |
| ||
| 4 |
∵a、b、c成等比数列，∴b2=ac，
由正弦定理可得sinAsinC=sin2B．
∴
| 1 |
| tanA |
| 1 |
| tanC |
| cosA |
| sinA |
| cosC |
| sinC |
| sinCcosA+cosCsinA |
| sinAsinC |
| sin(A+C) |
| sinAsinC |
| sinB |
| sin2B |
4
| ||
| 7 |
（Ⅱ）设
| BA |
| BC |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
由余弦定理可得：2=ac=b2=a2+c2-2accosB=a2+c2-2ac×
| 3 |
| 4 |
联立
|
|
|
即a=2，c=1，或a=1，c=2．
点评：本题考查了等比数列的性质、正弦定理与余弦定理、同角三角函数基本关系式，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
若幂函数y=（m2+3m-9）xm2-5的图象不过原点，则求m的值（ ）
| A、2 | B、-5 | C、2或-5 | D、-2 |
过棱长为2的正方体ABCD-A1B1C1D1的棱AD、CD、A1B1的中点E、F、G作截面，求：
在如图所示的组合体中，三棱柱ABC-A1B1C1的侧面ABB1A1是圆柱的轴截面，C是圆柱底面圆周上不与A、B重合的一个点．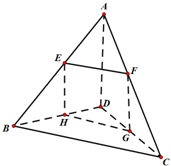
空间四边形ABCD中，AD=BC=a，与直线AD，BC都平行的平面分别交AB，AC，CD，BD于E，F，H．