题目内容
已知数列{an}的前n项和Sn=3n2-2n，求证：数列{an}是等差数列．
考点：等差关系的确定
专题：等差数列与等比数列
分析：首先根据数列{an}的前n项和Sn=3n2-2n，求出数列的首项，用Sn减去Sn-1，求出数列的通项，然后证明数列{an}是等差数列即可．
解答：
证明：当n＞1时，an=Sn-Sn-1=(3n2-2n)-[3（n-1）2-2（n-1）]=6n-5，
当n=1时，a1=s1=3-2=1也满足上式，
所以an=6n-5，
数列{an}的首项是1，an-an-1=（6n-5）-[6（n-1）-5]=6，
所以数列{an}是首项是1，公差是6的等差数列．
当n=1时，a1=s1=3-2=1也满足上式，
所以an=6n-5，
数列{an}的首项是1，an-an-1=（6n-5）-[6（n-1）-5]=6，
所以数列{an}是首项是1，公差是6的等差数列．
点评：本题主要考查了等差数列的判断以及通项的求法，属于基础题．
练习册系列答案
相关题目
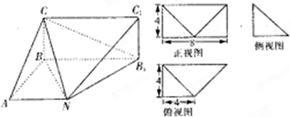已知某几何体的直观图和三视图如图所示，其正视图为矩形，侧视图为等腰直角三角表，俯视图为直角梯形．