题目内容
已知集合P={x|-2≤x≤5}，Q={x|k+1≤x≤2k-1}，当P∩Q=∅时，求实数k的取值范围．
考点：交集及其运算
专题：集合
分析：利用交集性质和不等式知识求解．
解答：
解：∵集合P={x|-2≤x≤5}，Q={x|k+1≤x≤2k-1}，P∩Q=∅，
∴当Q={x|k+1≤x≤2k-1}=∅时，
k+1＞2k-1，解得k＜2．
当Q={x|k+1≤x≤2k-1}≠∅时，
解得k＞4．
综上所述，实数k的取值范围（-∞，2）∪（4，+∞）．
∴当Q={x|k+1≤x≤2k-1}=∅时，
k+1＞2k-1，解得k＜2．
当Q={x|k+1≤x≤2k-1}≠∅时，
|
解得k＞4．
综上所述，实数k的取值范围（-∞，2）∪（4，+∞）．
点评：本题考查实数值的求法，是基础题，解题时要认真审题，注意交集性质和不等式知识的合理运用．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
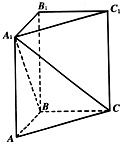在直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=1，BB1=2，求：