题目内容
已知函数f（x）=lnx+
ax2-2x存在单调递减区间，则实数a的取值范围为 ．
| 1 |
| 2 |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：利用导数进行理解，即f'（x）＜0在（0，+∞）上有解．可得ax2+2x-1＞0在正数范围内至少有一个解，结合根的判别式列式，不难得到a的取值范围．
解答：
解：对函数求导数，得f'（x）=
，（x＞0）
依题意，得f'（x）＜0在（0，+∞）上有解．即ax2-2x+1＜0在x＞0时有解．
①显然a≤0时，不等式有解，
②a＞0时，需满足△=4-4a＞0，解得a＜1，
综合①②得a＜1，
故答案为：（-∞，1）．
| ax2-2x+1 |
| x |
依题意，得f'（x）＜0在（0，+∞）上有解．即ax2-2x+1＜0在x＞0时有解．
①显然a≤0时，不等式有解，
②a＞0时，需满足△=4-4a＞0，解得a＜1，
综合①②得a＜1，
故答案为：（-∞，1）．
点评：本题主要考查函数与导数，以及函数与方程思想，体现了导数值为一种研究函数的工具，能完成单调性的判定和最值的求解方程，同时能结合常用数学思想，来考查同学们灵活运用知识解决问题的能力．
练习册系列答案
相关题目
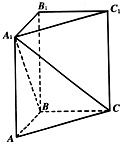在直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=1，BB1=2，求：