题目内容
若函数y=(m2-m-1)x-5m-3为幂函数,且是偶函数,则实数m的值为 .
考点:幂函数的概念、解析式、定义域、值域
专题:函数的性质及应用
分析:根据幂函数的定义,列出方程m2-m-1=1,求出m的值,再验证函数是否为偶函数即可.
解答:
解:∵函数y=(m2-m-1)x-5m-3为幂函数,且是偶函数,
∴m2-m-1=1,
即m2-m-2=0;
解得m=-1,或m=2;
当m=-1时,-5m-3=-5×(-1)-3=2,满足题意;
当m=2时,-5m-3=-5×2-3=-13,不满足题意,应舍去;
∴实数m的值为-1.
故答案为:-1.
∴m2-m-1=1,
即m2-m-2=0;
解得m=-1,或m=2;
当m=-1时,-5m-3=-5×(-1)-3=2,满足题意;
当m=2时,-5m-3=-5×2-3=-13,不满足题意,应舍去;
∴实数m的值为-1.
故答案为:-1.
点评:本题考查了幂函数的定义,也考查了偶函数的定义的应用问题,是基础题.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=n2-4n,第m项满足5<an<8,则m=( )
| A、9 | B、8 | C、7 | D、6 |
已知定义在R上的偶函数f(x)在区间[0,+∞)上是增函数,且f(1)=0,则不等式f(x)<0的解集为( )
| A、(-1,1) |
| B、(-∞,-1)∪(1,+∞) |
| C、(-1,0) |
| D、(0,1) |
设Sn是等差数列{an}的前n项和,若
=
,则
=( )
| a4 |
| a2 |
| 5 |
| 9 |
| S7 |
| S3 |
| A、1 | ||
| B、-1 | ||
| C、2 | ||
D、
|
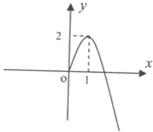 已知奇函数f(x)在[0,+∞)上的图象是如图所示的抛物线的一部分.
已知奇函数f(x)在[0,+∞)上的图象是如图所示的抛物线的一部分.