题目内容
1.以F1(-2,0),F2(2,0)为焦点的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(2,3).(1)求椭圆C的方程;
(2)过原点的直线l交椭圆C于M、N两点,P为椭圆C上的点,且与M、N不关于坐标轴对称,设直线MP、NP的斜率分别为k1,k2,试问:k1,k2的乘积是否为定值?若是,求出该定值,若不是,请说明理由.
分析 (1)由题意可得c=2,即a2-b2=4,将A(2,3)代入椭圆方程,解方程可得a,b,进而得到椭圆方程;
(2)由题意可设M(m,n),N(-m,-n),P(s,t),代入椭圆方程,作差,再由直线的斜率公式计算即可得到所求定值.
解答 解:(1)由题意可得c=2,即a2-b2=4,
将A(2,3)代入椭圆方程,可得$\frac{4}{{a}^{2}}$+$\frac{9}{{b}^{2}}$=1,
解得a=4,b=2$\sqrt{3}$,
即有椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1;
(2)由题意可设M(m,n),N(-m,-n),P(s,t),
可得$\frac{{m}^{2}}{16}$+$\frac{{n}^{2}}{12}$=1,$\frac{{s}^{2}}{16}$+$\frac{{t}^{2}}{12}$=1,
相减可得$\frac{(m-s)(m+s)}{16}$=-$\frac{(n-t)(n+t)}{12}$,
则k1•k2=$\frac{n-t}{m-s}$•$\frac{n+t}{m+s}$=-$\frac{12}{16}$=-$\frac{3}{4}$.
即有k1,k2的乘积为定值-$\frac{3}{4}$.
点评 本题考查椭圆的方程的求法,注意运用点满足方程,考查直线的斜率之积为定值问题,注意运用点差法,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
16.某大学生利用自己课余时间开了一间网店,为了了解店里某商品的盈利情况,该学生对这一商品20天的销量情况进行了统计,结果如下表所示:
已知此商品的进价为每个15元.
(1)根据上表数据,求这20天的日平均利润;
(2)若ξ表示销售该商品两天的利润和(单位:元),求ξ的分布列;
(3)若销售该商品两天的利润和的期望值不低于178元,则可被评为创业先进个人,请计算该大学生能否被评为创业先进个人?
| 售价(单位:元) | 23 | 21 | 20 |
| 日销量(单位:个) | 10 | 15 | 20 |
| 频数 | 4 | 14 | 2 |
(1)根据上表数据,求这20天的日平均利润;
(2)若ξ表示销售该商品两天的利润和(单位:元),求ξ的分布列;
(3)若销售该商品两天的利润和的期望值不低于178元,则可被评为创业先进个人,请计算该大学生能否被评为创业先进个人?
13.已知点M(-1,6),N(3,2),则线段MN的垂直平分线方程为( )
| A. | x-y-4=0 | B. | x-y+3=0 | C. | x+y-5=0 | D. | x+4y-17=0 |
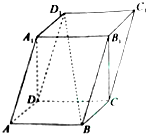 已知四棱柱ABCD-A1B1C1D1,侧面A1ADD1⊥面ABCD,底面ABCD是矩形,且AB=2,AD=1,AA1=$\sqrt{5}$,∠A1AD的余弦值为$\frac{\sqrt{5}}{5}$.
已知四棱柱ABCD-A1B1C1D1,侧面A1ADD1⊥面ABCD,底面ABCD是矩形,且AB=2,AD=1,AA1=$\sqrt{5}$,∠A1AD的余弦值为$\frac{\sqrt{5}}{5}$. 2016年里约奥运会和残奥会吉祥物的名字于2015年12月14日揭晓,两个吉祥物分别叫维尼修斯(Vinicius)和汤姆(Tom)(如图),以此纪念巴萨诺瓦曲风的著名音乐家Viniciusde Moraes和Tom Jobim.某商场在抽奖箱中放置了除图案外,其它无差别的8张卡片,其中2张印有“维尼修斯(Vinicius)”图案,n(2≤n≤4)张印有“汤姆(Tom)”图案,其余卡片上印有“2016年里约奥运会”的图案,
2016年里约奥运会和残奥会吉祥物的名字于2015年12月14日揭晓,两个吉祥物分别叫维尼修斯(Vinicius)和汤姆(Tom)(如图),以此纪念巴萨诺瓦曲风的著名音乐家Viniciusde Moraes和Tom Jobim.某商场在抽奖箱中放置了除图案外,其它无差别的8张卡片,其中2张印有“维尼修斯(Vinicius)”图案,n(2≤n≤4)张印有“汤姆(Tom)”图案,其余卡片上印有“2016年里约奥运会”的图案,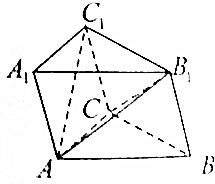 如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°.
如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°.