题目内容
12.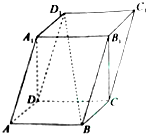 已知四棱柱ABCD-A1B1C1D1,侧面A1ADD1⊥面ABCD,底面ABCD是矩形,且AB=2,AD=1,AA1=$\sqrt{5}$,∠A1AD的余弦值为$\frac{\sqrt{5}}{5}$.
已知四棱柱ABCD-A1B1C1D1,侧面A1ADD1⊥面ABCD,底面ABCD是矩形,且AB=2,AD=1,AA1=$\sqrt{5}$,∠A1AD的余弦值为$\frac{\sqrt{5}}{5}$.(1)求证:平面A1DCB1⊥平面ABCD;
(2)求BD1与平面ABCD所成角的正切值.
分析 (1)利用余弦定理计算A1D,根据勾股定理的逆定理得出A1D⊥AD,又AD⊥CD,得出AD⊥平面A1DCB1,于是平面A1DCB1⊥平面ABCD;
(2)延长AD至E,使得AD=AE,连结D1E,则可证明D1E⊥平面ABCD,于是∠D1BE为BD1与平面ABCD所成的角,tan∠D1BE=$\frac{{D}_{1}E}{BE}$.
解答 证明:(1)∵AD=1,AA1=$\sqrt{5}$,cos∠A1AD=$\frac{\sqrt{5}}{5}$.∴A1D=$\sqrt{A{D}^{2}+{A}_{1}{A}^{2}-2AD•A{A}_{1}cos∠{A}_{1}AD}$=2.
∴AD2+A1D2=A1A2,∴A1D⊥AD.
∵四边形ABCD是矩形,∴AD⊥CD,
又A1D?平面A1DCB1,CD?平面A1DCB1,A1D∩CD=D.
∴AD⊥平面A1DCB1,∵AD?平面ABCD,
∴平面A1DCB1⊥平面ABCD.
(2)延长AD至E,使得AD=DE,连结D1E,BE,
∵DE=AD=A1D1,AD∥A1D1,
∴四边形A1DED1是平行四边形,∴D1E∥A1D,D1E=A1D=2.
∵侧面A1ADD1⊥面ABCD,侧面A1ADD1∩面ABCD=AD,A1D⊥AD,A1D?平面A1ADD1,
∴A1D⊥平面ABCD,
∴D1E⊥平面ABCD.
∴∠D1BE为BD1与平面ABCD所成的角.
∵AE=2AD=2,AB=2,∴BE=2$\sqrt{2}$,
∴tan∠D1BE=$\frac{{D}_{1}E}{BE}$=$\frac{2}{2\sqrt{2}}=\frac{\sqrt{2}}{2}$.
点评 本题考查了面面垂直的判定,线面角的计算,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知i为虚数单位,复数z满足$\frac{1+z}{1-z}$=i,则z2016=( )
| A. | -2i | B. | 2i | C. | -1 | D. | 1 |
17.设等差数列{an}的前n项和为Sn,已知a4+a6=-6,则S9=( )
| A. | -27 | B. | 27 | C. | -54 | D. | 54 |
4.已知函数f(x)是定义在R上的增函数,A(0,-1),B(3,1)是其图象上的两点,那么不等式-1≤f(x+1)≤1的解集是( )
| A. | [-1,2] | B. | (-∞,-1)∪(2,+∞) | C. | (-1,2) | D. | (-∞,-1]∪[2,+∞) |
2.复数z=|$\frac{\sqrt{3}-i}{i}$|-i(i为虚数单位),则复数z的共轭复数为( )
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |