题目内容
已知函数y=f（x）在R是奇函数且当x＞0时，f（x）=x2-2x-1，则x＜0，f（x）的解析式为f（x）= ．
考点：函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：由函数的奇偶性解函数的解析式，步骤是固定的．
解答：
解：当x＜0时，-x＞0，
∵函数y=f（x）在R是奇函数，
∴f（x）=-f（-x）
=-（（-x）2-2（-x）-1）
=-x2-2x+1，
故答案为：-x2-2x+1．
∵函数y=f（x）在R是奇函数，
∴f（x）=-f（-x）
=-（（-x）2-2（-x）-1）
=-x2-2x+1，
故答案为：-x2-2x+1．
点评：本题考查了借助函数的奇偶性求解函数的解析式，属于基础题．
练习册系列答案
相关题目
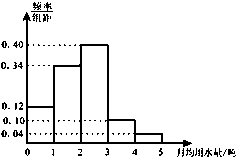如图是某城市通过抽样得到的居民某年的月均用水量（单位：吨）的频率分布直方图，其中分组区间为（0，1]，（1，2]，（2，3]，（3，4]，（4，5]．则由直方图可估计该城市居民月均用水量的众数是