题目内容
16.已知a,b∈R,i是虚数单位,若(a-i)(2+i)=bi,则a+bi=( )| A. | -$\frac{1}{2}$+$\frac{5}{2}$i | B. | -$\frac{1}{2}$-$\frac{5}{2}$i | C. | -$\frac{5}{2}$+$\frac{1}{2}$i | D. | -$\frac{5}{2}$-$\frac{1}{2}$i |
分析 利用是的乘法运算法则以及复数相等的充要条件求解即可.
解答 解:(a-i)(2+i)=bi,
可得2a+1+(a-2)i=bi,
解得a=-$\frac{1}{2}$,b=-$\frac{5}{2}$.
a+bi=-$\frac{1}{2}$-$\frac{5}{2}$i.
故选:B.
点评 本题考查复数的乘法运算法则以及复数的相等的充要条件,考查计算能力.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
6.某几何体的三视图细图所示,则该几何体的体积为( )
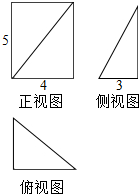

| A. | 12 | B. | 13 | C. | 18 | D. | 20 |
4.角速度为$\frac{π}{4}$的质点P从点(-1,0)逆时针沿单位圆x2+y2=1运动,经过17个时间单位后,点P的坐标是( )
| A. | ($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | B. | (-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
7.已知函数f(x)是定义在(0,+∞)上的单调函数,且对任意的正数x,y都有f(x•y)=f(x)+f(y),若正项数列{an}的前n项和为Sn,且满足f(Sn+2)-f(an)=f(3)(n∈N*),则a6=( )
| A. | $\frac{1}{2}×{({\frac{3}{2}})^6}$ | B. | $\frac{1}{2}×{({\frac{3}{2}})^5}$ | C. | ${({\frac{3}{2}})^5}$ | D. | ${({\frac{3}{2}})^6}$ |
8.下述函数中,在(-∞,0]内为增函数的是( )
| A. | y=x2-2 | B. | y=$\frac{3}{x}$ | C. | y=1+2x | D. | y=-(x+2)2 |