题目内容

要得到y=cos（2x-
π
3
）的图象，只需将函数y=sin（2x+
π
3
）的图象（　　）
A、向右平移
π
12
个单位
B、向左平移
π
12
个单位
C、向右平移
π
6
个单位
D、向左平移
π
6
个单位
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：利用三角函数的诱导公式把y=cos（2x-
π
3
）化为y=sin[2（x-
π
12
）+
π
3
]，然后由函数图象的平移原则得答案．
解答： 解：∵y=cos（2x-
π
3
）=sin（2x-
π
3
+
π
2
）=sin（2x+
π
6
）=sin[2（x-
π
12
）+
π
3
]，
∴要得到y=cos（2x-
π
3
）的图象，只需将函数y=sin（2x+
π
3
）的图象向右平移
π
12
个单位．
故选：A．
点评：本题考查了y=Asin（ωx+φ）的图象变换，三角函数的平移原则为左加右减上加下减．是基础题．
练习册系列答案
相关题目
若函数y=-|x-a|+b和y=|x-c|+d的图象交于点M（2，5）和N（8，3），则a+c的值为
 
．
某箱形几何体的三视图如图（侧视图中的圆弧是半圆），则该几何体的体积为
 
．
设等差数列{an}的前n项和为Sn，已知S4=-2，S5=0，则S6=（　　）
A、0B、1C、2D、3
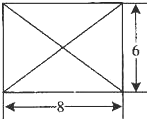已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为4的等腰三角形．则该几何体的体积为（　　）
A、48B、64C、96D、192
若a＞2，则方程
1
3
x3-ax2+1=0在（0，2）上恰好有（　　）
A、0个根B、1个根
C、2个根D、3个根
设a为实数，函数f（x）=x3+ax2+（a-3）x的导函数为f′（x），且f′（x）是偶函数，则曲线y=f（x）在原点处的切线方程为（　　）
A、y=3x+1
B、y=-3x
C、y=-3x+1
D、y=3x-3
若函数f（x）=ax3+bx2+cx+d（a≠0，x∈R）无极值点，则（　　）
A、b2≤3ac
B、b2≥3ac
C、b2＜3ac
D、b2＞3ac
等差数列{an}中，若S4≤4，S5≥15，则a4的最小值是（　　）
A、5B、6C、7D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网