题目内容
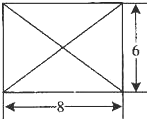已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为4的等腰三角形．则该几何体的体积为（ ）| A、48 | B、64 | C、96 | D、192 |
考点：棱柱、棱锥、棱台的体积
专题：综合题,空间位置关系与距离
分析：由题设可知，几何体是一个高为4的四棱锥，其底面是长、宽分别为8和6的矩形，正侧面及其相对侧面均为底边长为8，高为h1的等腰三角形，左、右侧面均为底边长为6、高为h2的等腰三角形，分析出图形之后，再利用公式求解即可．
解答：
解：由题设可知，几何体是一个高为4的四棱锥，其底面是长、宽分别为8和6的矩形，正侧面及其相对侧面均为底边长为8，高为h1的等腰三角形，左、右侧面均为底边长为6、高为h2的等腰三角形，如图所示．
所以几何体的体积为V=
•S矩形•h=
×6×8×4=64．
故选：B．
解：由题设可知，几何体是一个高为4的四棱锥，其底面是长、宽分别为8和6的矩形，正侧面及其相对侧面均为底边长为8，高为h1的等腰三角形，左、右侧面均为底边长为6、高为h2的等腰三角形，如图所示．所以几何体的体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
故选：B．
点评：本题考查的知识点是棱柱、棱锥、棱台的体积，其中根据已知的三视图分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
sin37°cos23°+cos37°sin23°的值是（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知条件p：x≠1或y≠2，条件q：xy≠2，那么￢p是￢q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
要得到y=cos（2x-
）的图象，只需将函数y=sin（2x+
）的图象（ ）
| π |
| 3 |
| π |
| 3 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
已知a，b为正实数，函数f（x）=ax3+bx+2在[0，1]上的最大值为4，则f（x）在[-1，0]上的最小值为（ ）
| A、0 | ||
B、
| ||
| C、-2 | ||
| D、2 |
设x∈R，2 x2-1＞4则不等式的解是（ ）
A、x≠±
| ||||
B、-
| ||||
| C、-2＜x＜2 | ||||
D、x＞
|
已知函数f（x）=x3+bx2+cx+d（b、c、d为常数），当x∈（0，1）时取得极大值，当x∈（1，2）时取极小值，则（b+
）2+（c-3）2的取值范围是（ ）
| 1 |
| 2 |
A、（
| ||||
B、（
| ||||
C、（
| ||||
| D、（5，25） |