题目内容
已知双曲线
-
=1(a>0,b>0),圆(x-1)2+y2=4被双曲线的一条渐近线截得的弦长为
,则此双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 15 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先根据双曲线方程求得其中一条渐近线方程,根据题意可知圆心到渐近线的距离为
,进而表示出圆心到渐近线的距离,求得a,b的关系,即可求出双曲线的离心率.
| 1 |
| 2 |
解答:
解:依题意可知双曲线的一渐近线方程为bx-ay=0,
∵弦长为
,圆的半径为2,
由弦长的一半、半径和圆心到直线的距离构成直角三角形,
则圆心到渐近线的距离d=
=
,
即
=
,即a2=3b2,
∴c2=b2+a2=4b2=
a2,
∴双曲线的离心率为e2=
,
∴双曲线的离心率为e=
.
故选:B
∵弦长为
| 15 |
由弦长的一半、半径和圆心到直线的距离构成直角三角形,
则圆心到渐近线的距离d=
22-(
|
| 1 |
| 2 |
即
| |b| | ||
|
| 1 |
| 2 |
∴c2=b2+a2=4b2=
| 4 |
| 3 |
∴双曲线的离心率为e2=
| 4 |
| 3 |
∴双曲线的离心率为e=
2
| ||
| 3 |
故选:B
点评:本题主要考查了双曲线的简单性质.解题的关键是利用圆中弦长的一半、半径和圆心到直线的距离构成直角三角形,求得圆心到渐近线的距离.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数f(x)=
(a,b∈R)定义域为R,则3a+b的取值范围是( )
| (a+2)x2+bx+a+2 |
| A、[-2,+∞) |
| B、[-6,+∞) |
| C、[6,+∞) |
| D、[0,+∞) |
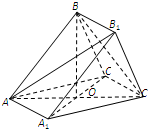 如图所示,三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面A1ACC1,
如图所示,三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面A1ACC1,