题目内容
如果函数f（x）=(
)|x|（-∞＜x＜+∞），那么函数f（x）是（ ）
| 1 |
| 2 |
| A、奇函数，且在（-∞，0）上是增函数 |
| B、偶函数，且在（-∞，0）上是减函数 |
| C、奇函数，且在（0，+∞）上是增函数 |
| D、偶函数，且在（0，+∞）上是减函数 |
考点：函数奇偶性的判断,函数单调性的判断与证明
专题：计算题,函数的性质及应用
分析：定义域为R，关于原点对称，计算f（-x），与f（x）比较，即可得到奇偶性，讨论x＞0，x＜0，运用指数函数的单调性，即可得到结论．
解答：
解：定义域为R，关于原点对称，f（-x）=(
)|-x|=f（x），
则为偶函数，当x＞0时，y=（
）x为减函数，则x＜0时，则为增函数，
故选D．
| 1 |
| 2 |
则为偶函数，当x＞0时，y=（
| 1 |
| 2 |
故选D．
点评：本题考查函数的奇偶性和单调性的判断，考查指数函数的单调性，属于基础题．
练习册系列答案
相关题目
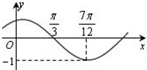函数f（x）=Acos（ωx+φ）（A＞0，ω＞0）的图象如图所示，为了得到g（x）=Acosωx的图象，可以将f（x）的图象（ ）A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
以直线x-2y=0和x+2y-4=0的交点为圆心，且过点（2，0）的圆的方程为（ ）
| A、（x-2）2+（y-1）2=1 |
| B、（x+2）2+（y+1）2=1 |
| C、（x-2）2+（y-1）2=2 |
| D、（x+2）2+（y+1）2=2 |